構造計画研究所 構造計画研究所 SBDプロダクツサービス部
SBDエンジニアリング部

お気軽にお問い
合わせください

構造計画研究所 構造計画研究所

お問い合わせ

COLUMN

技術コラム

  • ホーム
  • 【構造】製品設計/強度設計の基本講座シリーズ　vol.9　物理量の時間変化

【構造】製品設計/強度設計の基本講座シリーズ　vol.9　物理量の時間変化

2021年03月04日

前回まで、運動の定義から変形/応力/ひずみを考えてきました。
連続体力学では、更に、運動及び運動している物理量の時間変化を考える必要が出てきます。
この時、時間微分を考えますが、必然的に物質点に着目しながら時間変化を観測することになります。
この演算操作は対象とする関数について、物質点 X を固定しておいて時間 ｔ で微分することになります。

物質表示の時間微分

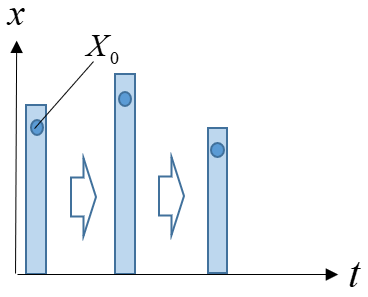
右図の様に、棒の長さが時間変化する時、棒のある点 X0 における物理量 Θ （例えば温度）の時間変化を考えます。

物質点 X0 の微小移動ベクトル　ΔΓ は、Δt から t0+Δt の間に Δt だけ変化しますが、物質点 X0 自体は時間変化しません。

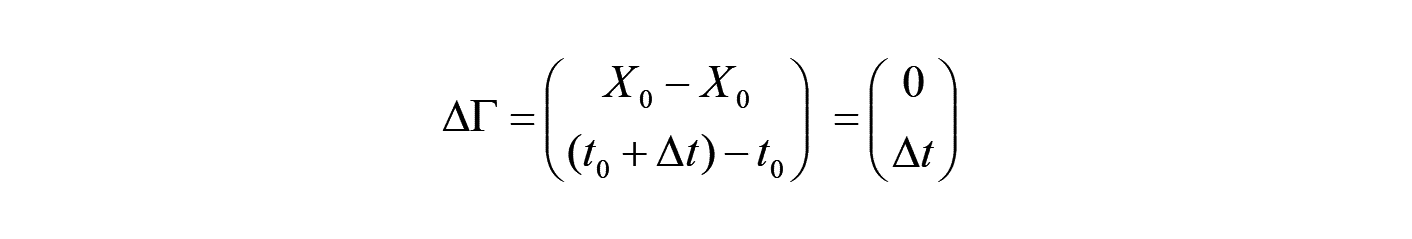
この時、 X0 物理量 Θ の変化 ΔΘ は、テイラー展開の１次の項で線形化すれば、以下となります。

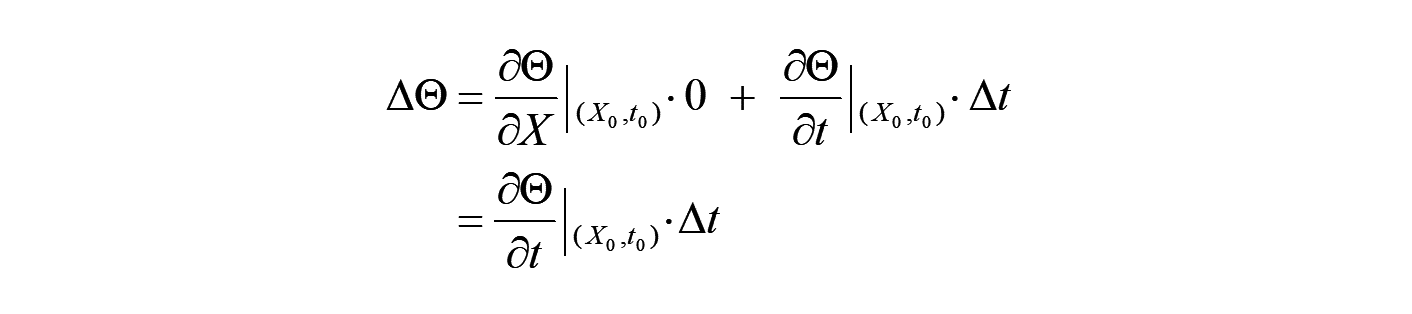
ここで、Δt → 0 の時、以下の微分の関係を得ます。

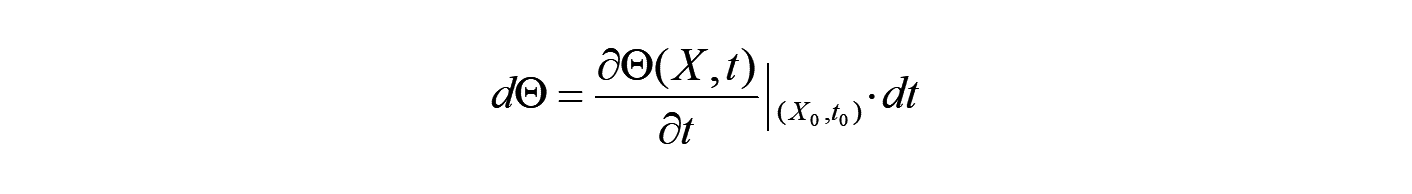
よって、この微分商 dΘ/dt が物理量 Θ の物質表示における時間微分演算となり、物質時間微分と呼びます。

物質表示の物質時間微分


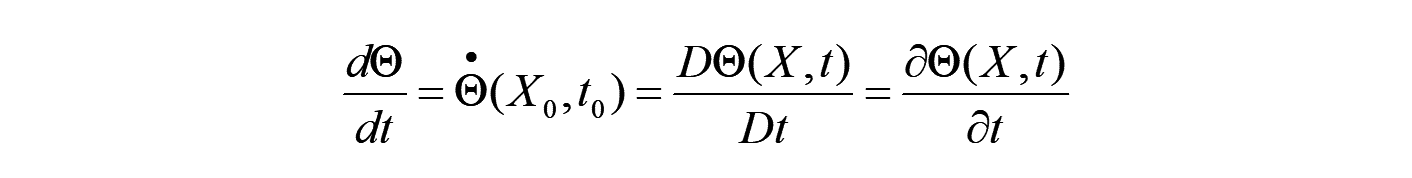
空間表示の時間微分

空間表示された物質点 X0 の物理量 θ(x , t) は、棒の伸び縮みによって、空間位置 x が時間変化することを考慮する必要があります。
この時、物質点 X0 の微小移動ベクトル Δγ は、以下となります。

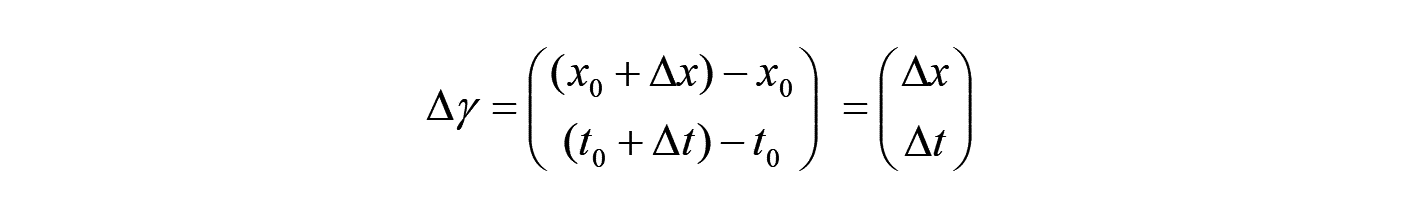
すると、 X0 上の物理量 θ の変化 Δθ は、やはり、テイラー展開の１次の項で線形化すれば、以下となります。

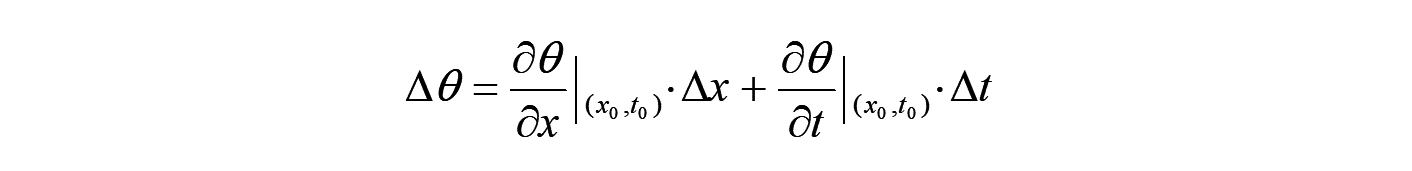
ここで、Δt → 0 の時、 Δx は物質点 X0 の運動の結果として決まり、時間に依存していることを考えて、以下の速度 V の1次式で表現します。

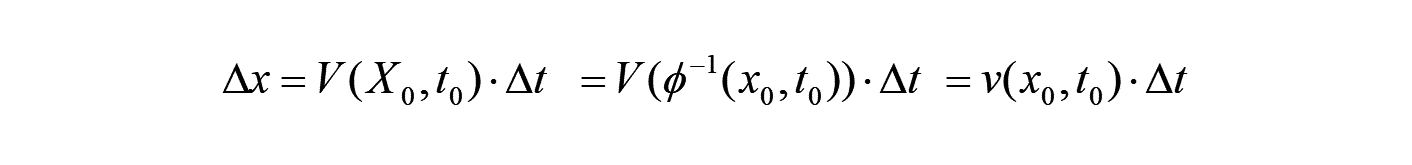
のように空間表示にしてから、以下の微分の関係を得ます。

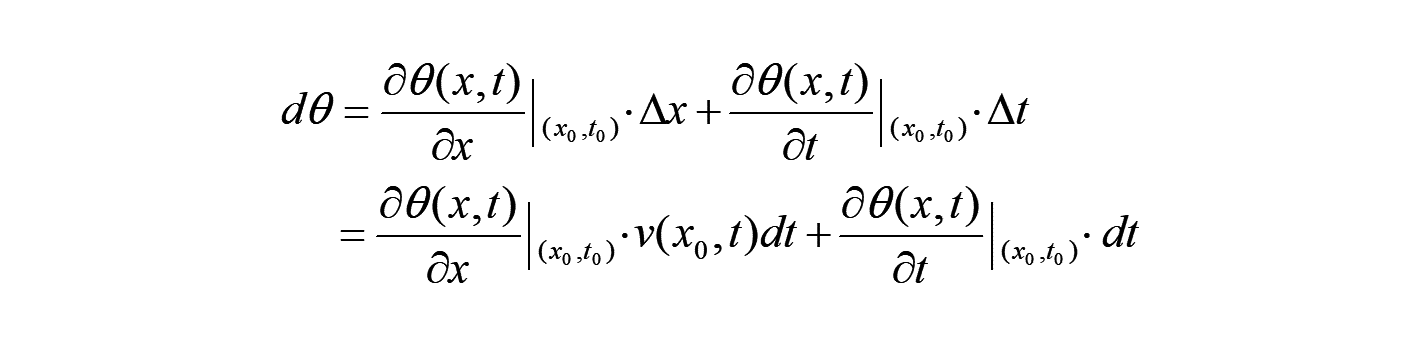
よって、この微分商 dθ/dt が物理量 θ の空間表示における時間微分となります。
下式の第2項は、物理量の空間微分と速度ベクトルの内積となり 移流項 と呼ばれます

空間表示の物質時間微分


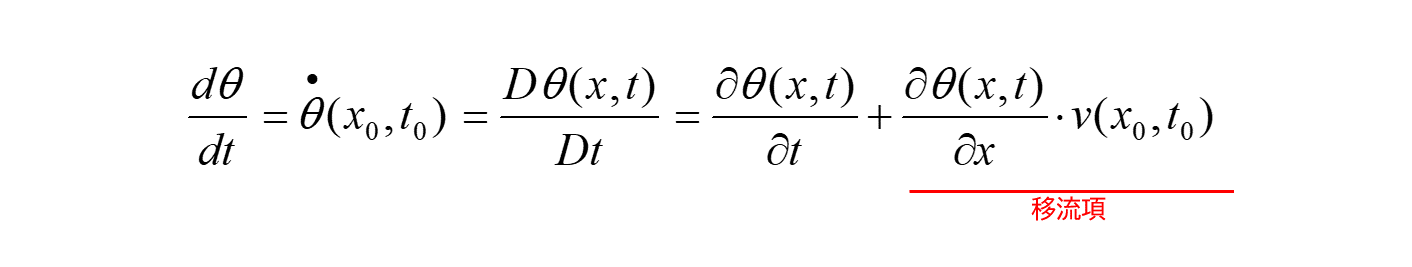
物質時間微分は、物質点を固定して（変形、流れに乗って）時間変化を見るもので、物理的な現象の記述方法になります。
これを固定座標（オイラーメッシュ）で記述しようとすると移流項という非線形の項が現れてしまいます。

[From N. Sahashi]

SBDメールマガジン新規登録

第1・第3木曜日配信！
SBDメールマガジンより、
最新の技術コラムをお届けします。

\

お問い合わせ

前のコラム | 変形モードの比較 技術コラム一覧 次のコラム | 運動や変形の速さを示すには

Analysis Case
解析事例

Analysis Case
解析事例

キーワード

もっと詳しい条件で検索する　▼

全体カテゴリ

製品カテゴリ

業種・⽤途

リセット

Topics
トピックス

イベント・セミナー

シミュレーションに関するイベント・セミナー情報をお届けいたします。

もっと見る

トレーニング

SBD製品各種の操作トレーニングを開催しております。

もっと見る

技術コラム

シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。

もっと見る

Topics
トピックス

イベント・セミナー

シミュレーションに関するイベント・セミナー情報をお届けいたします。

もっと見る

トレーニング

SBD製品各種の操作トレーニングを開催しております。

もっと見る

技術コラム

シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。

もっと見る

お問い合わせ

03-5342-1046 受付時間／平日9:00～17:00 お問い合わせフォーム