お気軽にお問い
前回まで、ひずみの定義について紹介してきました。
ここでは、有限ひずみと微小ひずみの違いについて、いくつかの変形モードについて具体的に比較してみます。
COLUMN
技術コラム
【構造】製品設計/強度設計の基本講座シリーズ vol.8 変形モードの比較
伸び変形モードについて
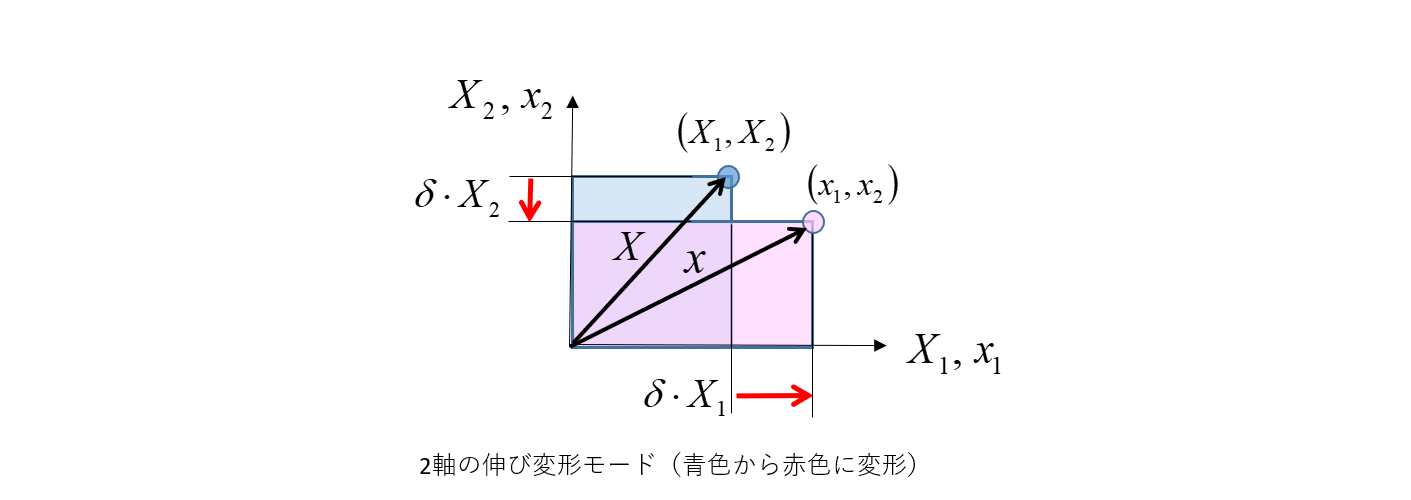
運動は、 ｘ＝Φ（X） であり、変位ベクトルは u＝ｘーX となります。
上図のように各方向に δ の変形率が生じた場合、以下となります。
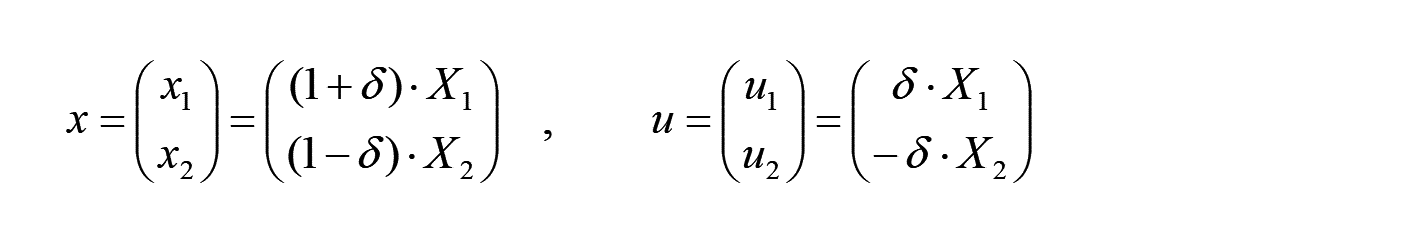
よって、変形勾配、及び、微小ひずみは
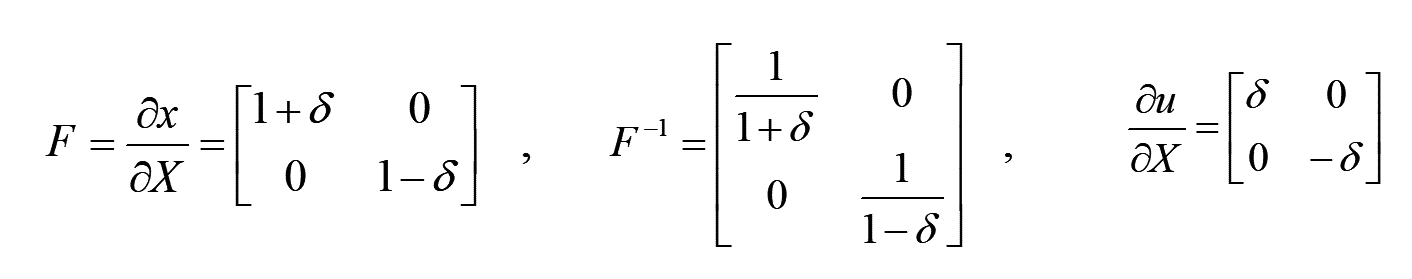
よって、先の各種ひずみの定義式より、
微小ひずみは、各方向に δ の１乗の項ですが、クリーンひずみは δ の2乗の項が追加されています。
また、オイラーひずみは変形後の長さで割ったかたちになっています。
δ を0.1（10%）、0.01（1%）として具体的に計算すれば、それぞれ以下となります。
ひずみ量が大きくなると、各ひずみの違いが顕著になります。
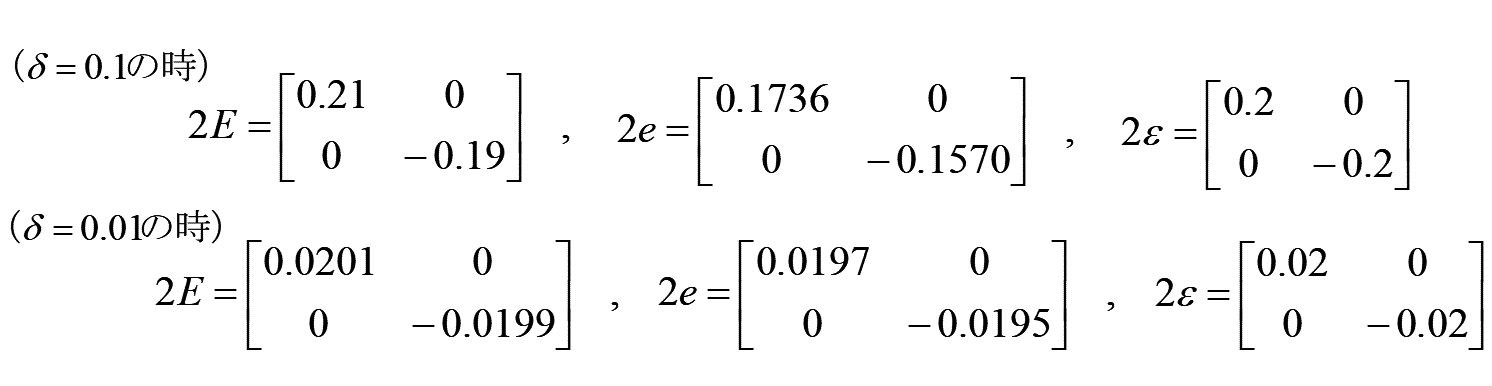
せん断変形モードについて
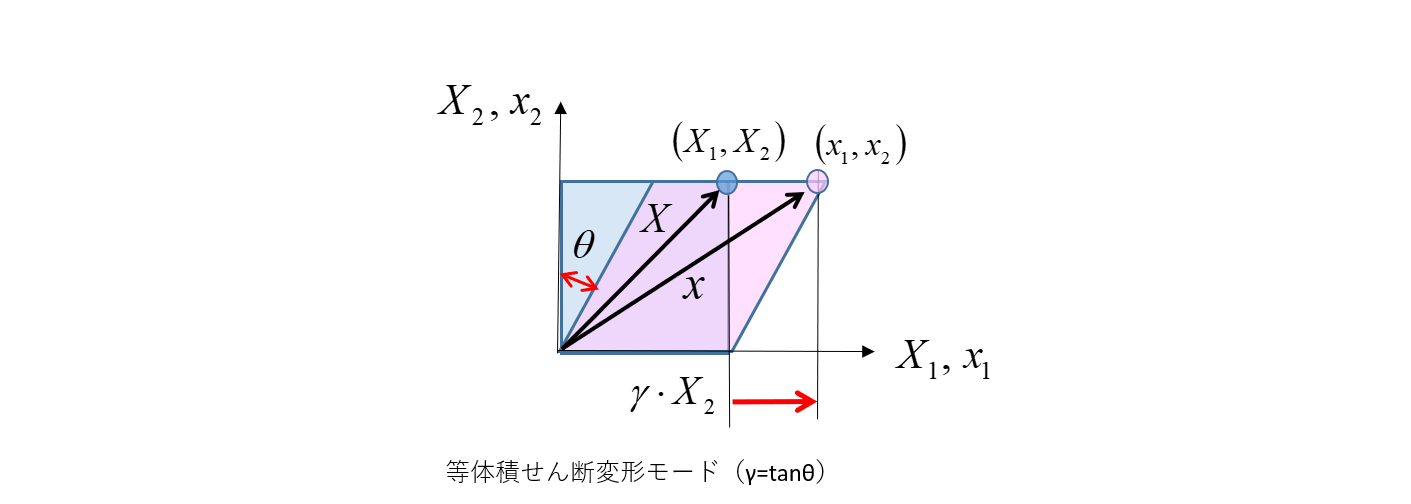
上図のせん断変形の場合、 ｘ と ｕ は、以下で表されます。
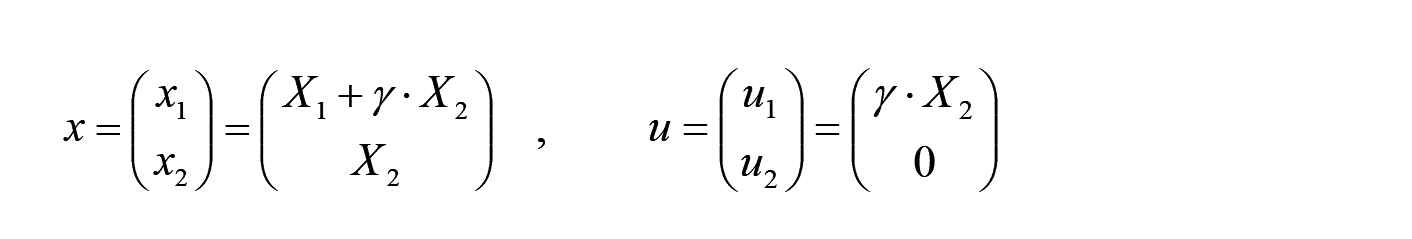
よって、変形勾配、及び、微小ひずみは
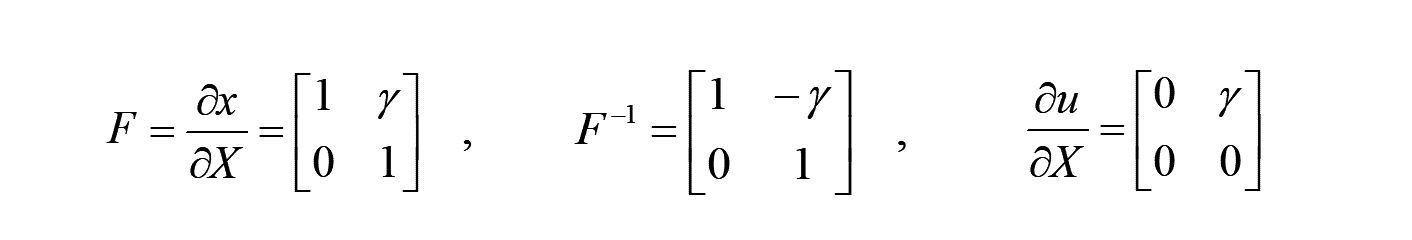
よって、先の各種ひずみの定義式より、以下となります。
微小ひずみはせん断成分のみですが、有限ひずみでは、せん断による 方向の伸びが考慮されています。
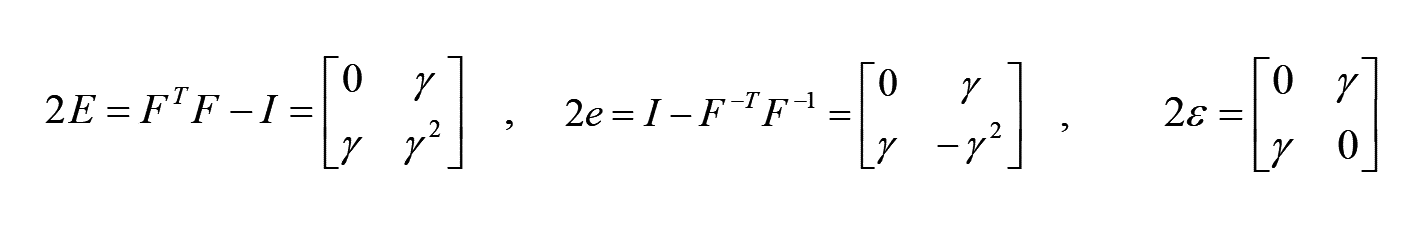
剛体回転モードについて
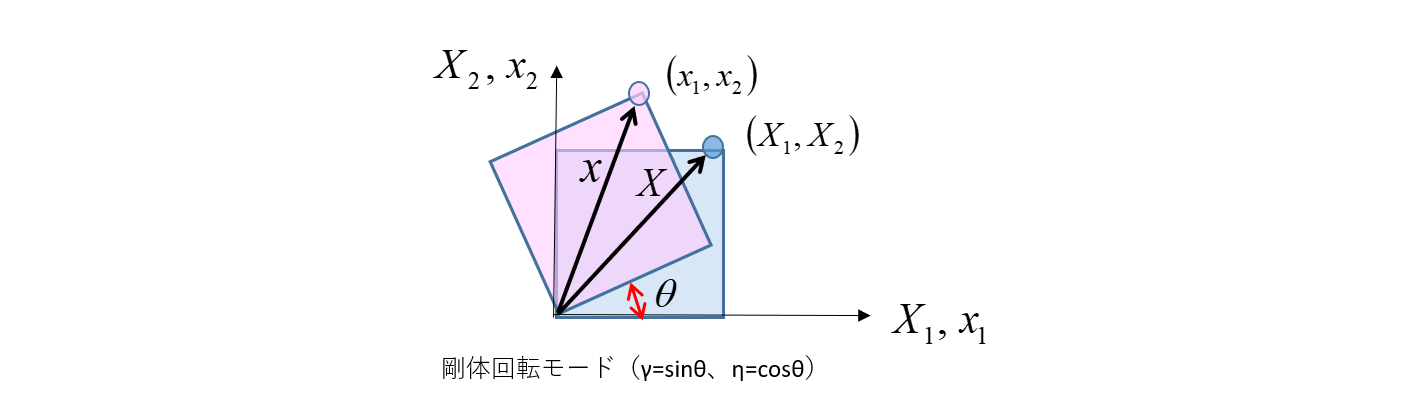
上図の剛体回転の場合、 ｘ と ｕ は、以下で表されます。
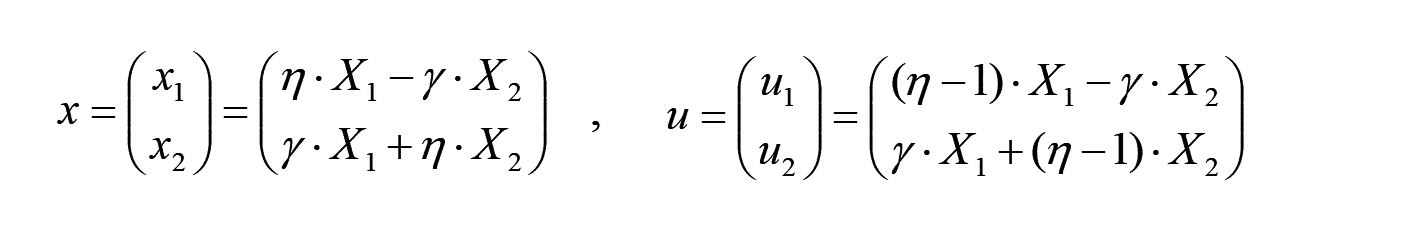
よって、変形勾配、及び、微小ひずみは
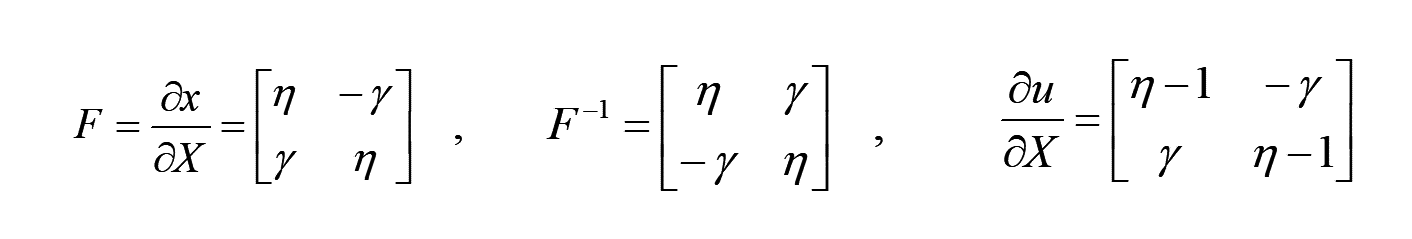
よって、先の各種ひずみの定義式より、以下となります。
有限ひずみでは、剛体回転によるひずみは０になりますが、微小ひずみでは回転によって伸びが計算されてしまいます。
微小ひずみでは、回転によるひずみを正しく計算できないことがわかります。
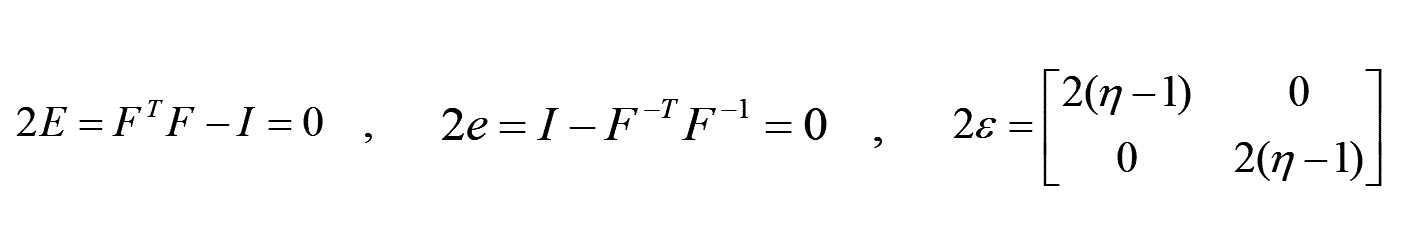
[From N. Sahashi]
第1・第3木曜日配信！
SBDメールマガジンより、
最新の技術コラムをお届けします。
Analysis Case
解析事例
Analysis Case
解析事例
解析事例
Topics
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2024年10月08日
2024年08月27日
2024年08月26日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2024年10月01日
2024年10月01日
2024年09月24日
Topics
トピックス
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2024年10月08日
2024年08月27日
2024年08月26日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2024年10月01日
2024年10月01日
2024年09月24日
