前回、物理量の時間変化を表す物質時間微分について紹介しました。
今回は、物理量と共に変化する運動や変形の速さ(時間微分)を考えます。
COLUMN
技術コラム
【構造】製品設計/強度設計の基本講座シリーズ vol.10 運動や変形の速さを示すには
速度の定義(運動の物質時間微分)
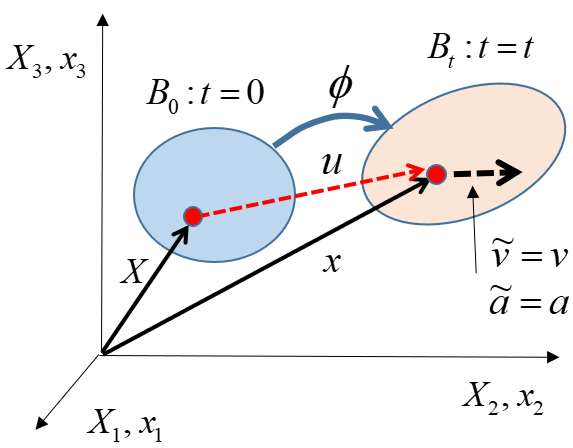
まず、運動の定義を確認します。
基準配置 にある物質点 が、時刻 において占めている空間配置 内の位置 を与える式
 を再度確認します(右図参照)。
を再度確認します(右図参照)。
その物質時間微分は、以下となります。
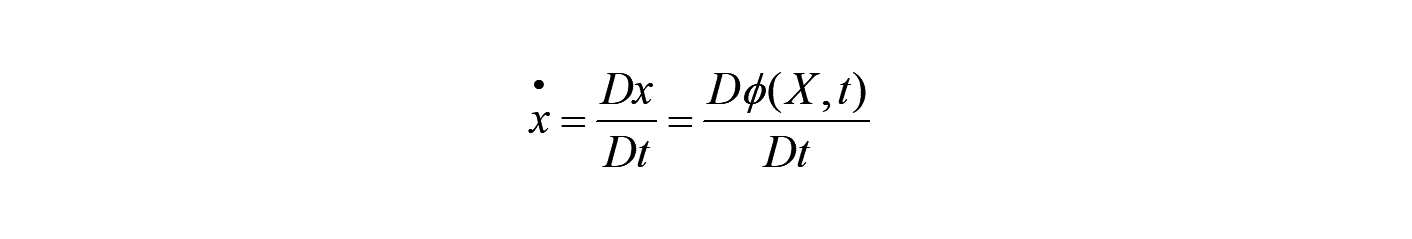
これは元々物質表示の関数なので、以下となります。
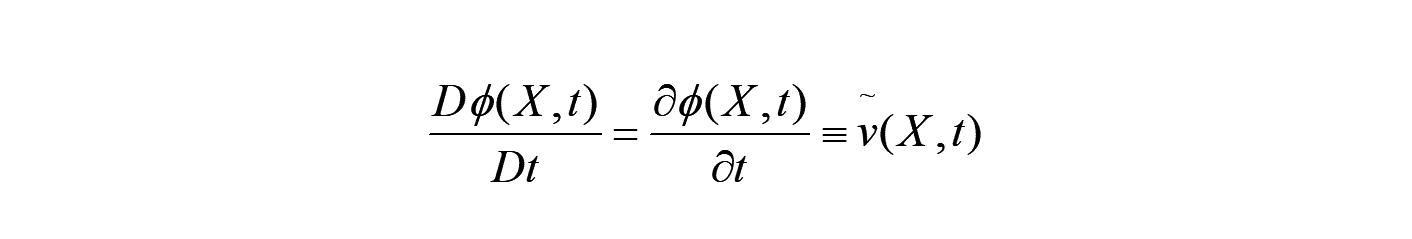
ここで、 は物質点 の速度ベクトルと呼ばれます。
は物質点 の速度ベクトルと呼ばれます。
速度ベクトルは、基準配置 を参照している 点の定義ですが、同時に空間配置 の 点が占める位置の時間変化率でもあるので、 と同義に考えることができます(運動の2階微分として加速度も同様に定義できます)。
と同義に考えることができます(運動の2階微分として加速度も同様に定義できます)。
変形勾配テンソルの物質時間微分
変形勾配テンソル は、運動  の勾配として、以下の様に定義されました。
の勾配として、以下の様に定義されました。
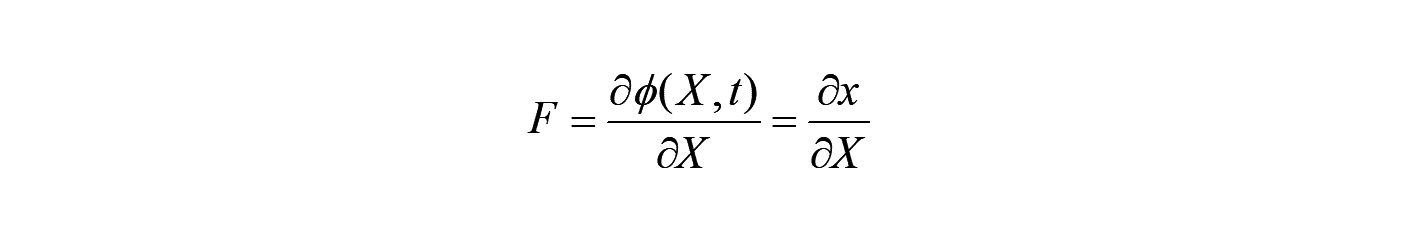
この時、 の物質時間微分を考えると、微分の順番を変えて、以下を得ます。
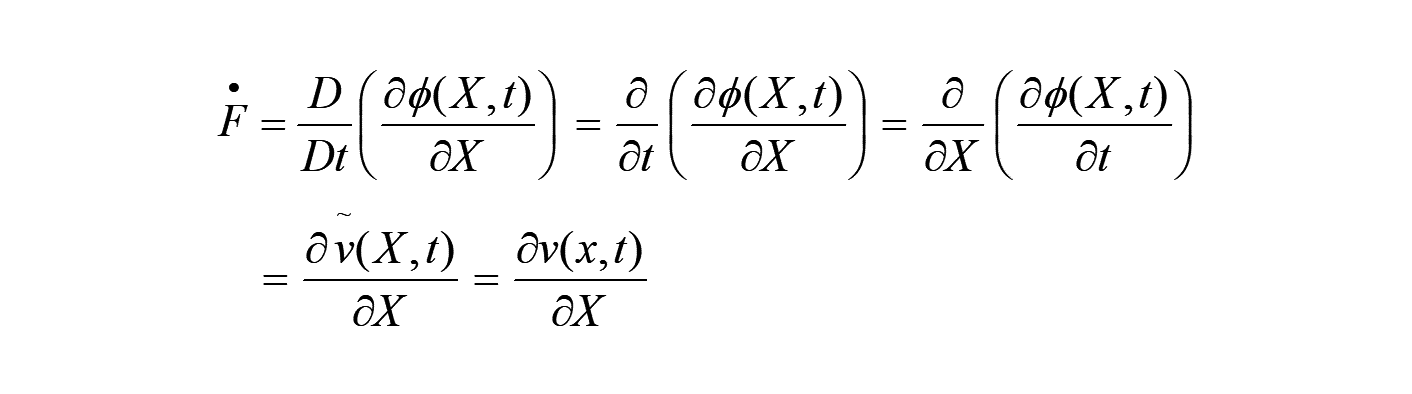
すなわち、変形勾配の物質微分  は、速度ベクトルの物質座標に関する勾配となります。
は、速度ベクトルの物質座標に関する勾配となります。
また、  を以下の様に変形させます。
を以下の様に変形させます。
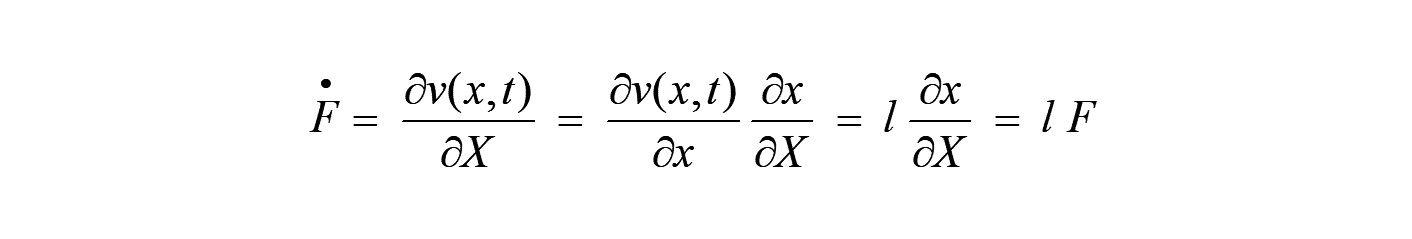
ここで、  を速度勾配テンソルと呼ばれます。
を速度勾配テンソルと呼ばれます。
ある時刻 の現在配置 における速度ベクトル場 とすれば、その全微分を与える式は以下となり、
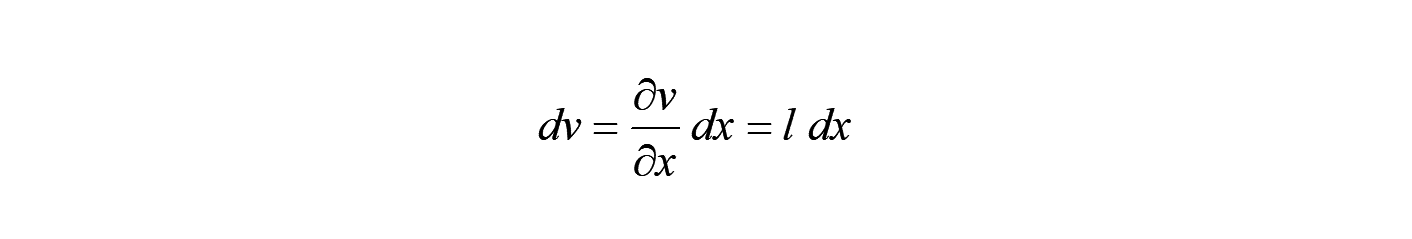
(速度勾配テンソル)は 点近傍のベクトル を速度の微分ベクトルに変換する2階のテンソルの意味にもなります。
更に、 を対称部分と反対称部分に分解して、 の作用を考えてみます。
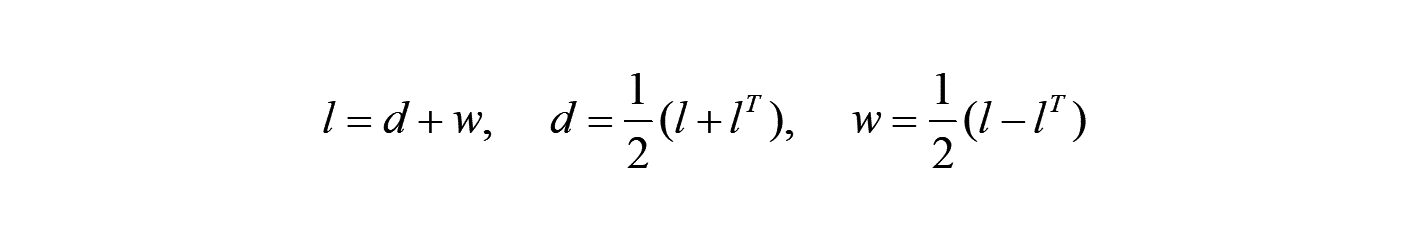
ここで、 は変形速度テンソル、 はスピンテンソルと呼ばれます。
成分表示すれば、以下となります。
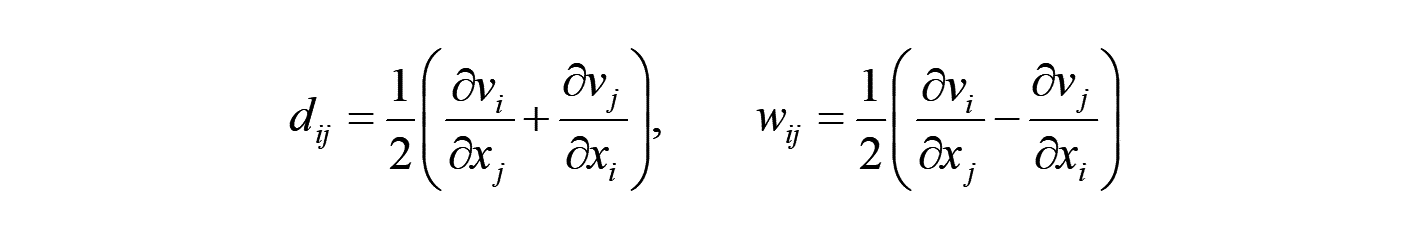
この式は、微小ひずみの式と同等で、変位量が速度になっています。
しかし、 のような微小変形仮定はなく、あくまで現在配置内の点 がまさに変形しようとしている速度増分を表しています。
のような微小変形仮定はなく、あくまで現在配置内の点 がまさに変形しようとしている速度増分を表しています。
の対角項は、各軸方向の変形速度(単位時間当たりの長さ変化)、非対角項は各軸回りの角度変化率(単位時間当たりの角度変化)を示します。
特にの非対角項はスピンテンソルという名前の様に回転角速度を示します。
次回、もう少し時間積分について考えていきます。
[From N. Sahashi]
第1・第3木曜日配信!
SBDメールマガジンより、
最新の技術コラムをお届けします。
Analysis Case
解析事例
Analysis Case
解析事例


解析事例
Topics
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2025年09月30日
2025年09月29日
2025年09月13日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2025年10月14日
2025年10月14日
2025年09月19日
Topics
トピックス


トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2025年09月30日
2025年09月29日
2025年09月13日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2025年10月14日
2025年10月14日
2025年09月19日






