お気軽にお問い
前回は、変形勾配テンソル F を使って、物質点 X 近傍の微小ベクトル ΔX と、変形後の Δx の関係を定義しました。
今回は前回定義した微小ひずみに対し、ストレッチ分を表す変形前後のスカラー量の変化率を抽出する有限ひずみを定義を見ていきます。
COLUMN
技術コラム
【構造】製品設計/強度設計の基本講座シリーズ vol.7 有限ひずみ
体積の変化率ヤコビアン
今、基準配置 の一つの物質点 X 近傍において、3つの微小ベクトル 、 、 で定義される微小平行六面体を考えます。
すると、変形後の現在配置 での微小六面体は、以下の３つの微小ベクトルで定義されることになります。
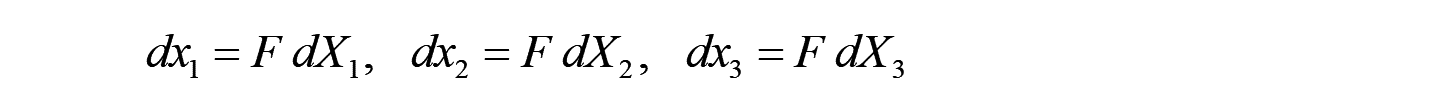
３つのベクトルからなる平行六面体の体積は、スカラー三重積の公式によって、以下のように定義されます。
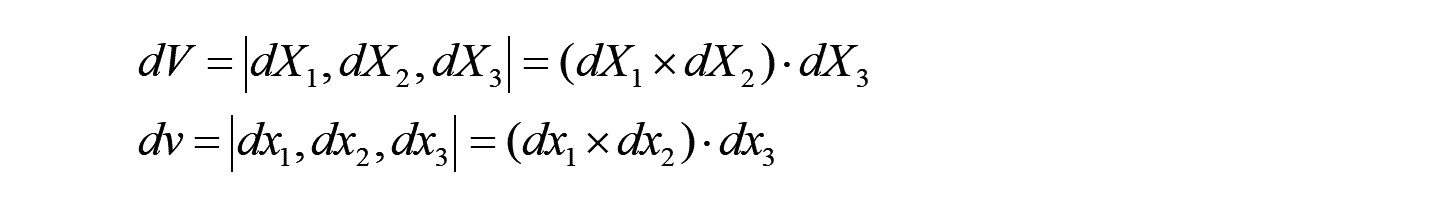
また、上記の両者の関係は、スカラー三重積の性質を使って、以下に変形できます。
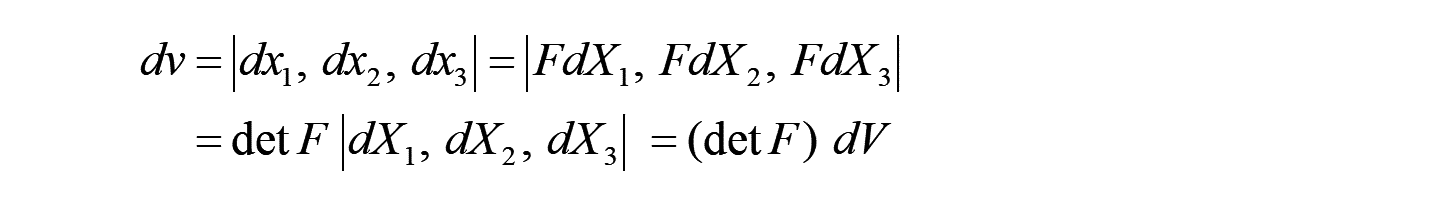
とすれば、
となり、Jを ヤコビアン といいます。
Jは微小体積の変化率を表し、変形中に体積がなくなったり負になることはないので、J＞0となります。
J＝１ のときは体積変化なしの非圧縮変形となります。
面積の変化率
次に、２つの微小ベクトルで定義される以下のベクトルを考えます。これを面積ベクトルと定義します。
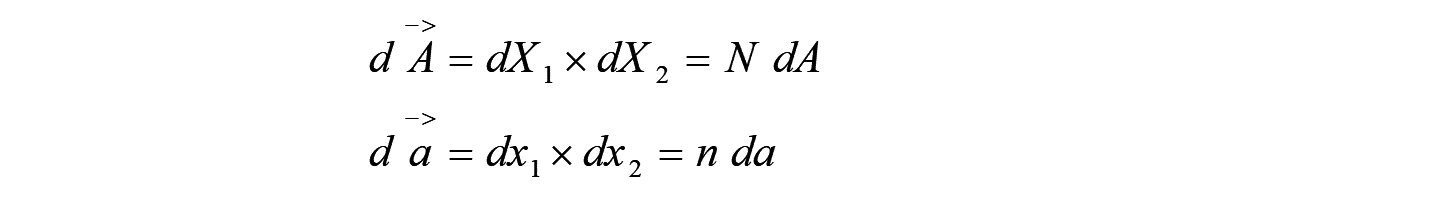
~ ここで、N,ｎは、２つのベクトルでつくる面に垂直な単位法線ベクトル ~
前述の体積の定義から、変形後の微小体積の式は、以下のように記述できます。
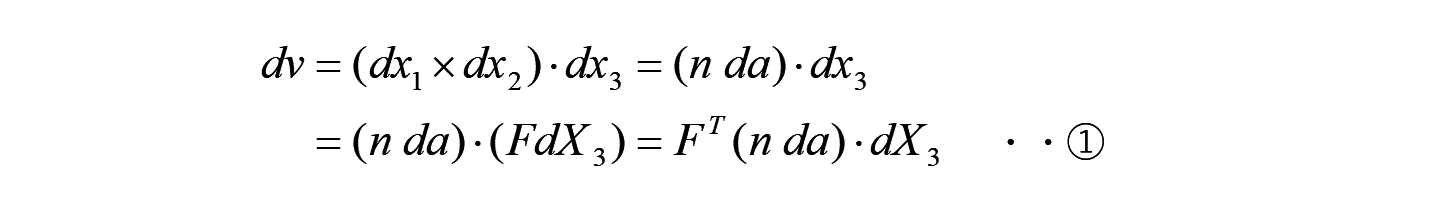
一方、
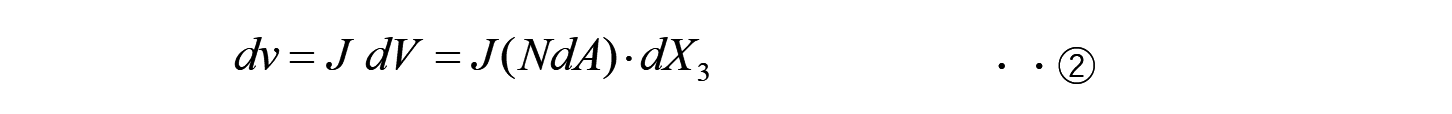
となり、この①、②の式より、
よって、 
の関係を得ます。ここで は変形勾配テンソルの逆行列の転置行列となります。
スカラーである面積の変化率は、以下の関係となり、やはり変形勾配テンソルを用いて定義されます。
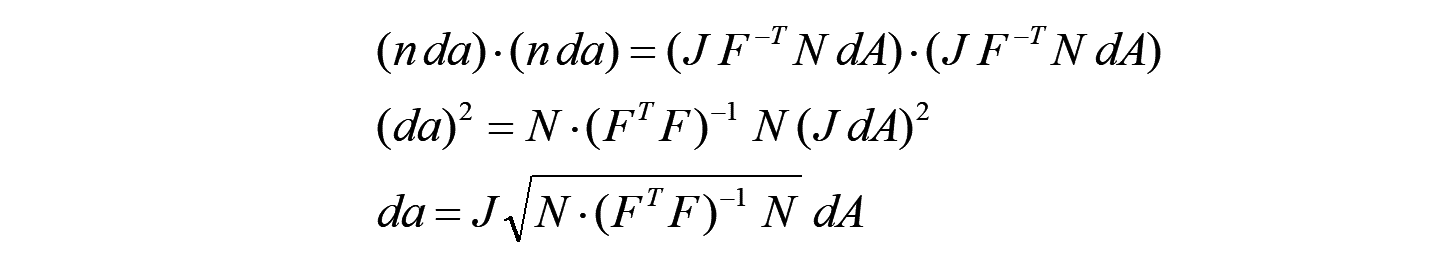
よって、
の関係を得ます。
有限ひずみの定義
このように、変形勾配テンソルによって、微小ベクトル、微小面積、微小体積の変化率を計算できます。
しかし、この変形勾配テンソルには、ベクトルの回転とストレッチを含むものとなっているので、ストレッチ分を表す変形前後のスカラー量の変化率を抽出するために、ベクトルの２乗（ノルム）の変化を定義します。
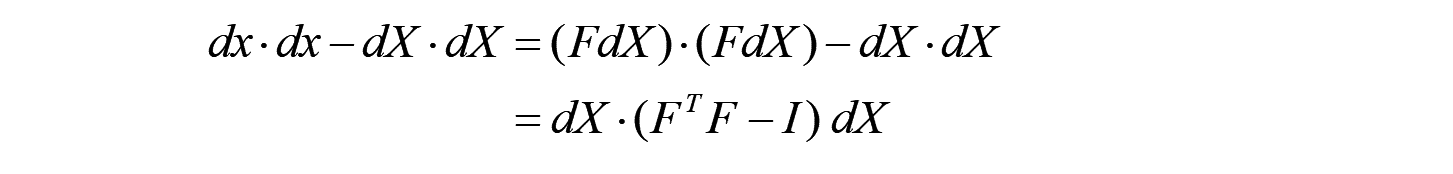
同様に、以下のようにも定義できます。
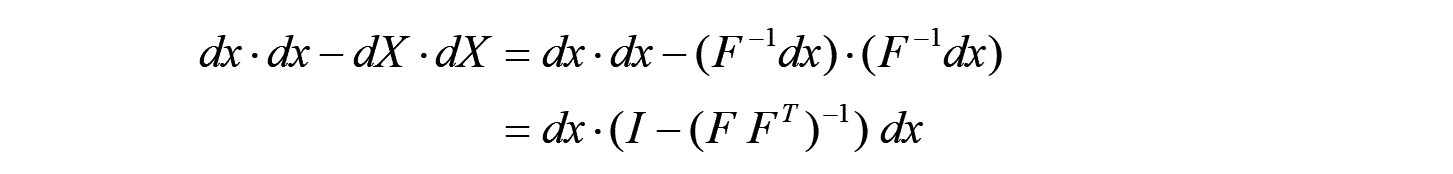
これは、局所的な変形による微小線素の長さの変化率、すなわち、ひずみを表しています。
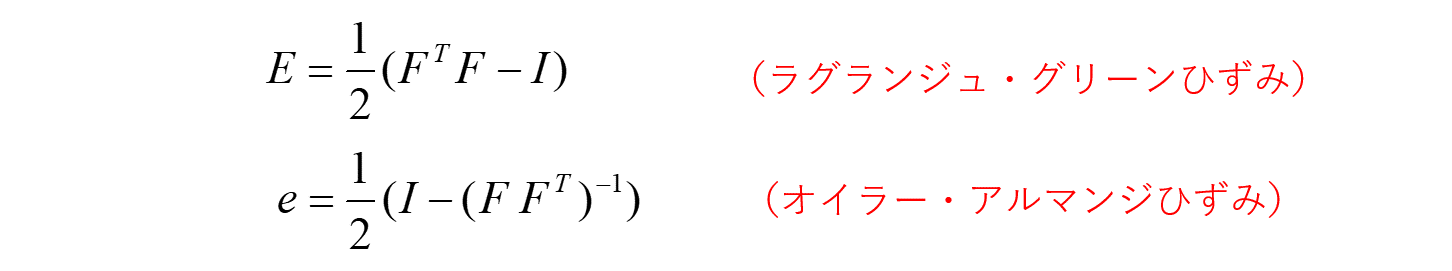
と定義し、微分ベクトルの長さ S の変化を
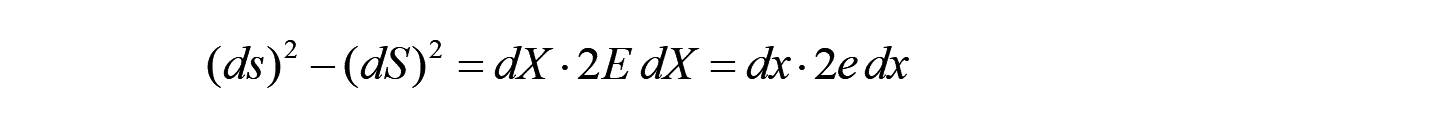
のように２次形式によってひずみを定義する２階のテンソル量となります。
前回の時に定義した微小ひずみに対して、有限ひずみとも呼ばれます。
[From N. Sahashi]
第1・第3木曜日配信！
SBDメールマガジンより、
最新の技術コラムをお届けします。
Analysis Case
解析事例
Analysis Case
解析事例
解析事例
Topics
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2024年10月08日
2024年08月27日
2024年08月26日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2024年10月01日
2024年10月01日
2024年09月24日
Topics
トピックス
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2024年10月08日
2024年08月27日
2024年08月26日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2024年10月01日
2024年10月01日
2024年09月24日
