お気軽にお問い
前回、微小ひずみの定義を行いましたが、物体の運動の定義から、より汎用性のある変形/ひずみの定義を考えます。
COLUMN
技術コラム
【構造】製品設計/強度設計の基本講座シリーズ vol.6 ひずみの汎用定義
物体の運動
下図のように、物質点の集合としての物体 が、時刻 t 後に
の集合に変化したとします。
時刻 ｔ=0 における の初期状態を基準配置とします。
その時、各点の初期配置を位置ベクトル X で定義します。
時刻 ｔ 後に、X の移動後の位置ベクトルを x と定義し、この x が占める集合を現在配置 とします。
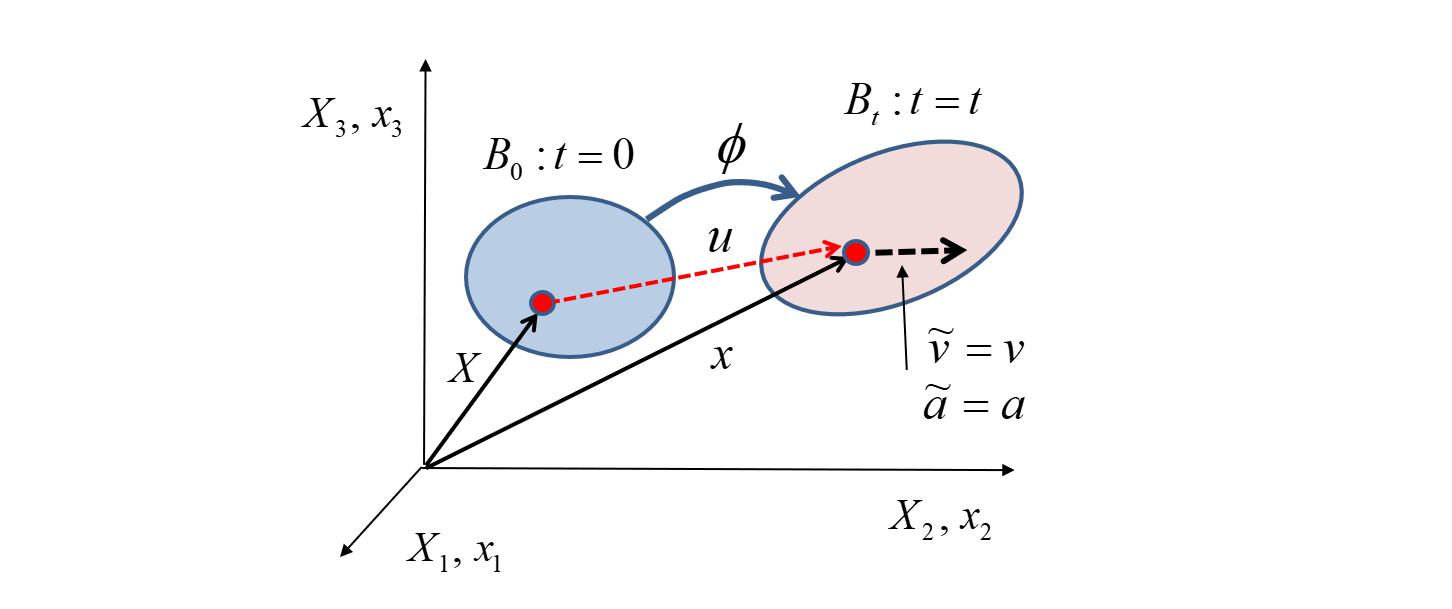
このとき X と x の関係は、写像関数 Φ を用いて、以下のように表されます。
移動中に集合体が重なったり、分離されず滑らかに変化したとすると、 Φ は１対１対であり
逆関数が定義できますので、以下の関係も定義されます。
Φ(X,t) は、すべての物質点の動きを定義しており、「運動」を表していると言えます。
変位ベクトル、速度ベクトル、加速度ベクトル
次に、各点の変位 
は、運動 Φ を使って、以下のように定義できます。
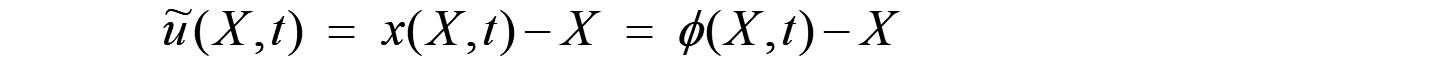
この引き算の結果は、基準配置からの移動量を表すベクトル量であり変位ベクトルと言います。
変位ベクトルを現在配置（空間表示）すれば、
となります。但し、両者は、表示が違うだけで同じベクトル量を表しています。
各点の速度 
は、運動 Φ の時間変化率であり、以下のように定義できます。
これは、時刻 ｔ における物質点 A の速度ベクトルとなります。
上式は基準配置 の表示になっていますが、物理的意味からして、下式のように現在配置 のベクトル表示にすると都合が良く、速度ベクトルと言います。
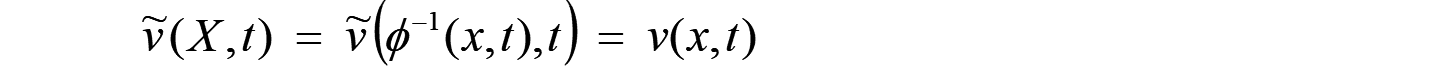
更に、速度 の時間変化率は加速度となります。以下のように加速度ベクトルが定義できます。
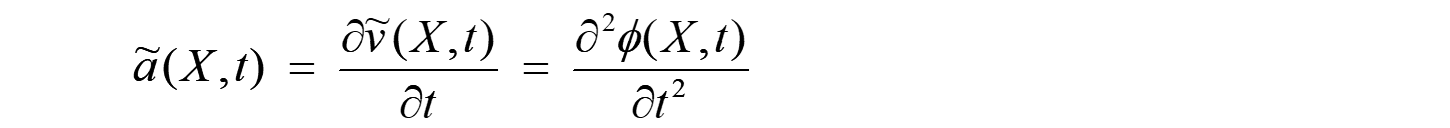
上式も基準配置 の表示になっていますが、物理的意味からして、下式のように現在配置 のベクトル表示にすると都合が良く、加速度ベクトルと言います。
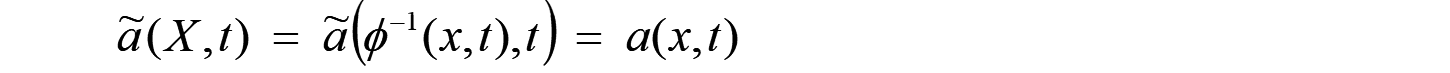
変形勾配テンソルとは
再び、下図の状況を示します。
変位ベクトルは運動を表していて、物体の移動は分かりますが、これだけでは、連続体の変形の様子はわかりません。
変形は、移動だけでなく移動点近傍の移動の仕方の違いを観測する必要があります。
そのため、物質点 X とその近傍 X+ΔX 点の運動の違いを変形前後で定義します。
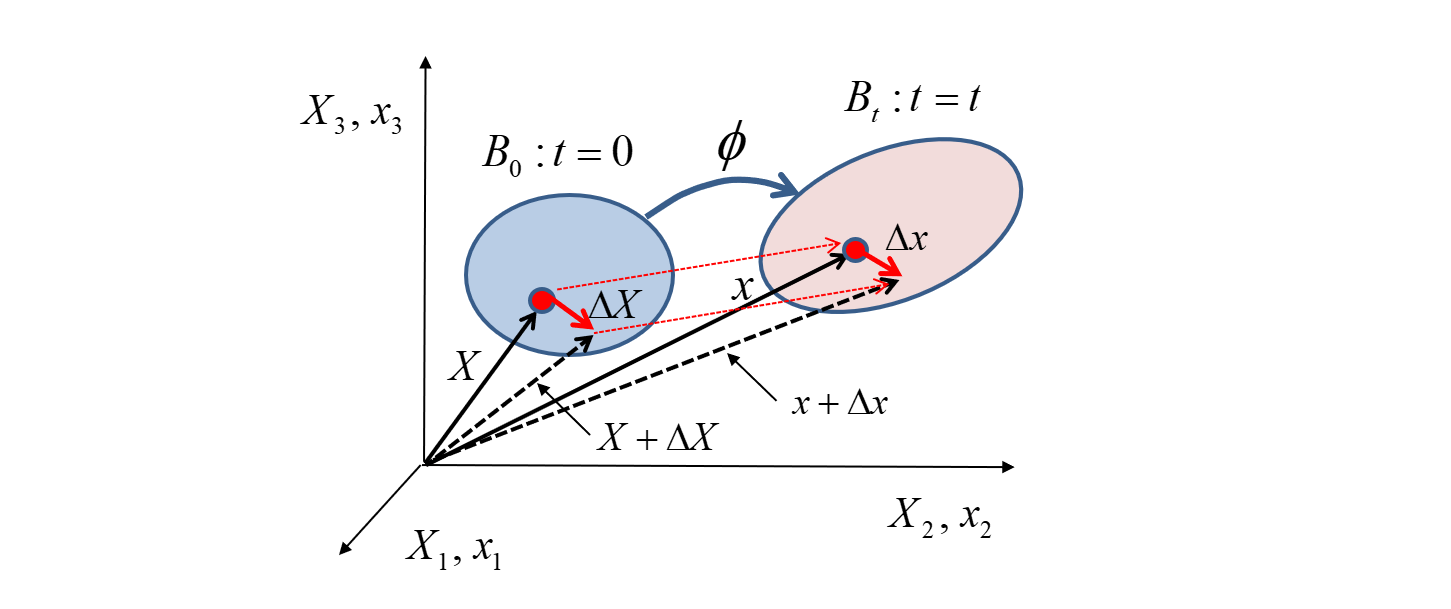
図のように、それぞれの点が現在配置 における以下の位置に移動することになります。
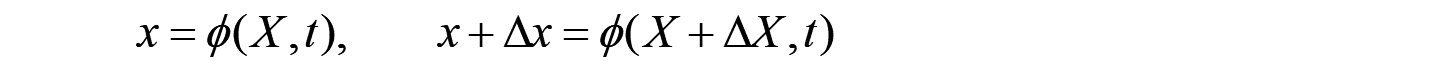
この時、Δｘは微小近傍点として、以下の様にテイラー展開の１次（線形項）で近似できます。
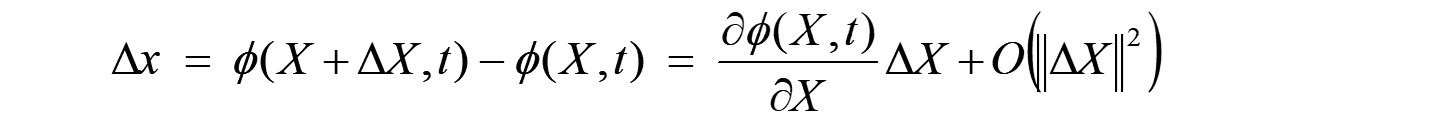
更に全微分表示すれば、以下となります。
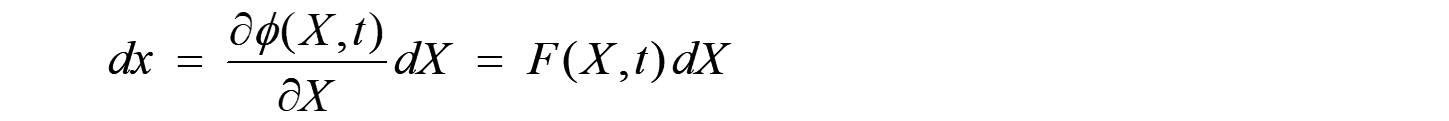
F(X,t)によって、X 近傍の微分ベクトル dX が dx に変換されることを示しています。
すなわち、 X 近傍の変位の違いを示しており、変形（後々ひずみに）に関係するテンソル量となり、変形勾配テンソルと呼ばれます。
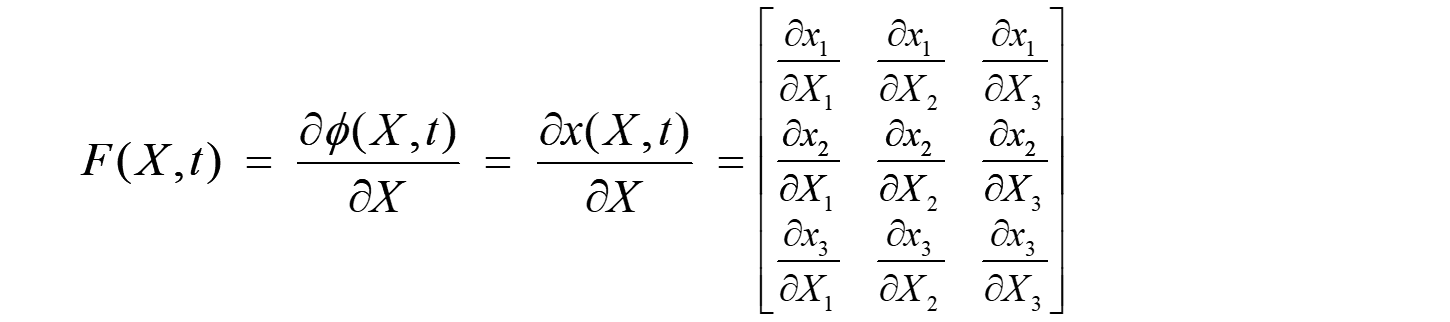
この変形勾配テンソルにより、ひずみの定義が行われますが、次回に紹介します。
[From N. Sahashi]
第1・第3木曜日配信！
SBDメールマガジンより、
最新の技術コラムをお届けします。
Analysis Case
解析事例
Analysis Case
解析事例
解析事例
Topics
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2024年10月08日
2024年08月27日
2024年08月26日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2024年10月01日
2024年10月01日
2024年09月24日
Topics
トピックス
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2024年10月08日
2024年08月27日
2024年08月26日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2024年10月01日
2024年10月01日
2024年09月24日
