【構造最適化】目的関数　vol.2　剛性最大化と最大ミーゼス応力最小化

2021年02月18日

前回は剛性最大化について触れました。
今回は目的関数としての最大ミーゼス応力最小化について書いてみます。
まずは簡単に用語の整理から始めます。

『目的関数』と『制約関数』について

『目的関数』とは剛性最大化、最大ミーゼス応力最小化、最大変位最小化など、特定の関数の値を最大または最小にする、といったものになります。
一方、『制約関数』とは、最大ミーゼス応力が5 MPa以下、最大変位が0.2 mm以下など、特定の関数の値の範囲を指定するものになります。

従って、『目的関数としての最大ミーゼス応力最小化』は、ある制約条件のもとで最大ミーゼス応力が最も小さくなる形状を求めるものであり、『制約関数としての最大ミーゼス応力の規定』は、具体的に指定した値以下にしなさいという意味で、両者は似て非なるものです。

『目的関数としての最大ミーゼス応力最小化』について

最大ミーゼス応力の最小化問題において、領域内の最大ミーゼス応力は次のように表されます。

(2.1)

ここで、

σ_{M}

はミーゼス応力、

σ_{a}

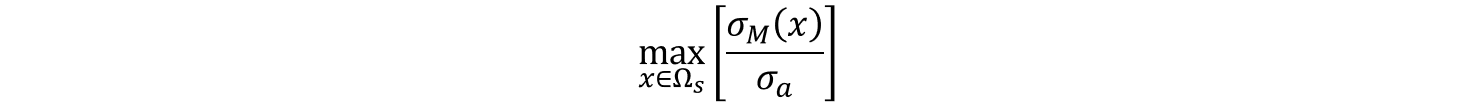
は規格化のための定数を表します。
この値を最小化することが目的となるわけですが、このままでは局所的に微分不可能となる可能性もありますので、次のように積分系に変形して扱います。

(2.2)

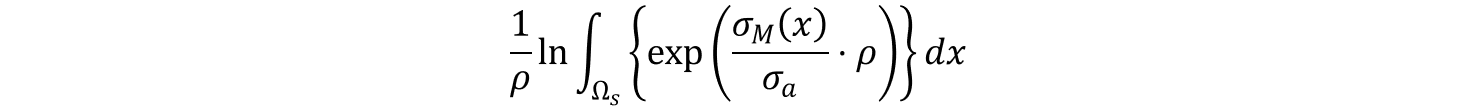
次のようなデータ(Table 1)に対して、式(2.2)を適用した結果を見てみましょう。

Table 1　10個のデータ

Table 2　結果

Table 2に示したように、ρの値を大きくするにつれて、Table 1のデータの中で最大値となる5番目の値に近い数字を抽出できています。
このようにして抽出した値が最小となるように、形状を変更していくのが『目的関数としての最大ミーゼス応力最小化』です。

『目的関数としての剛性最大化』との違いについて

前回の記事でも述べた通り、剛性最大化では実際に応力を見ているのではなく、物体に蓄えられたひずみエネルギーの最小化を目的関数に置き換えて計算しています。
それに比べて、今回ご説明した最大ミーゼス応力最小化では、抽出された最大値の部分にフォーカスして、その部分の応力を下げるような目的関数となっています。

従って、局所的に改善したい部分がある場合は最大ミーゼス応力最小化を、全体的に改善したい場合には剛性最大化と、適切に使い分けることによって、より目的に即した解析結果が得られます。

次回予告

次回はトポロジー最適化と形状最適化を組み合わせた事例をご紹介します。

[From K.Takabatake]

データID	値
1	0.319924707
2	0.664908535
3	0.667030147
4	0.351031789
5	1
6	0.436483894
7	0.621835531
8	0.307769955
9	0.592795642
10	0.06014546

ρ	値
1	2.84
5	1.12
10	1.01
50	1.00
100	1.00

全体カテゴリ

製品カテゴリ

Topics
トピックス

SBDプロダクツサービス部
SBDエンジニアリング部

技術コラム