COLUMN

技術コラム

【構造最適化】目的関数　vol.1　剛性最大化について

2021年02月04日

今回からは、今までの記事と毛色を変えて、少し理論寄りの内容も書き進めてまいります。

構造最適化に限らず、最適化の計算では目的関数と制約関数を設定し、制約関数を満たす範囲内で目的関数が最大または最小となる変数の値を求めます。
構造最適化では、目的関数として剛性最大化や最大ミーゼス応力最小化などが挙げられ、過去の記事でもこれらを目的とした事例を紹介してまいりました。

剛性の最大化と最大ミーゼス応力の最小化は、言葉としては理解できます。
意味合いとしては似ているような気がしますが、構造最適化の計算において、やっていることは全く異なります。
今回は、この2つの目的関数の違いについて触れてみます。

いきなり剛性最大化とは何かについて触れる前に、まずは前段として、用語の整理を行います。

『剛性』について

『剛性』は物体の変形のしにくさを表す指標です。
簡単な例としてバネの一端を固定し、反対側に引っ張り荷重を載荷した場合を考えます。
この時、バネの伸びと作用する力の関係については、式(1.1)に示すフックの法則で記述できます。

(1.1)

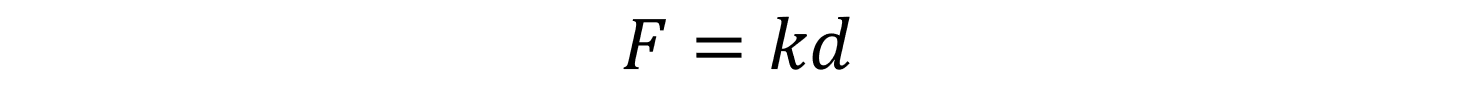
ここで、F は力、k はバネ定数、d は伸びを表します。
式(1.1)を次のように変形してみましょう。

(1.2)

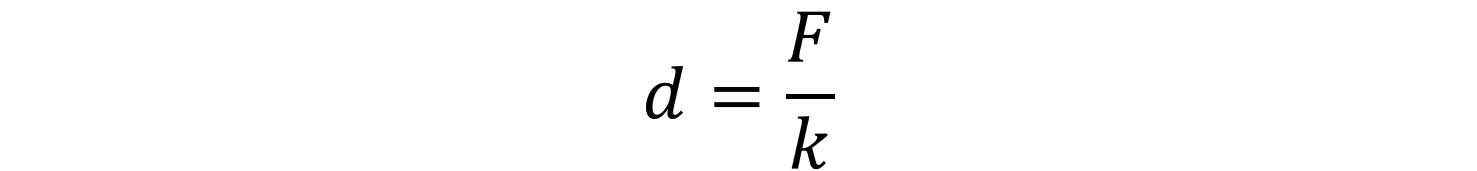
式(1.2)から明らかなように、バネ定数が大きくなると、同じ力が作用していても伸びは小さくなります。
つまり、バネ定数はバネの変形しにくさを意味し、バネの剛性といえます。

有限要素法では、全体の構造を要素間の結合に分割して計算します。
このとき、解くべき剛性方程式は次式(1.3)で記述できます。

(1.3)

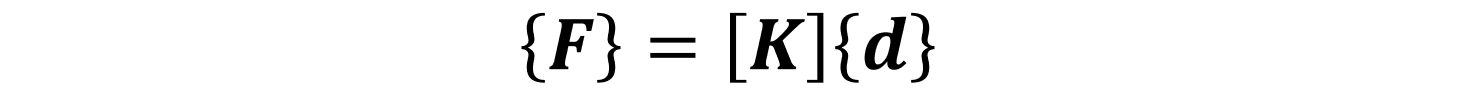
ここで、Kは剛性マトリックスを表します。
先ほどと同様に考えれば、Kを最大化することができれば、剛性はもっとも強くなるはずです。

では、剛性マトリックスの最大化とは何でしょう。
いきなりこの問題に触れる前に、『ひずみエネルギー』について述べたいと思います。

『ひずみエネルギー』について

物体に対して外力が働き、静的な釣り合いにあるとするならば、外力がなす仕事は内部に『ひずみエネルギー』として蓄えられます。
(簡単のため、垂直応力による弾性変形のみ生じているとして議論を進めます。) まずは長さ l、断面積 A の棒で考えてみます。
棒に対して力が作用し、伸びが生じているとしましょう。
この時、棒に蓄えられるエネルギーは、棒に対する仕事と等しくなります。
従って、ひずみエネルギーは次式(1.4)で求めることができます。

(1.4)

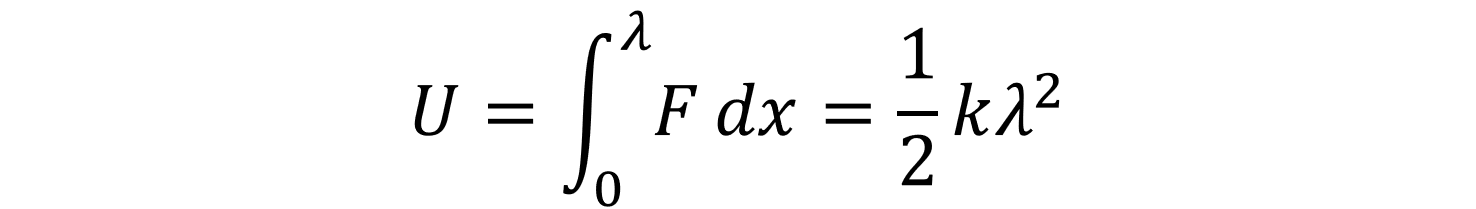
ここで、U はひずみエネルギー( 弾性エネルギーともいう )、λ はバネの伸びを表します。
さて、伸びが λ のときの荷重を P とすると、式(1.4)は次式のように変形できます。

(1.5)

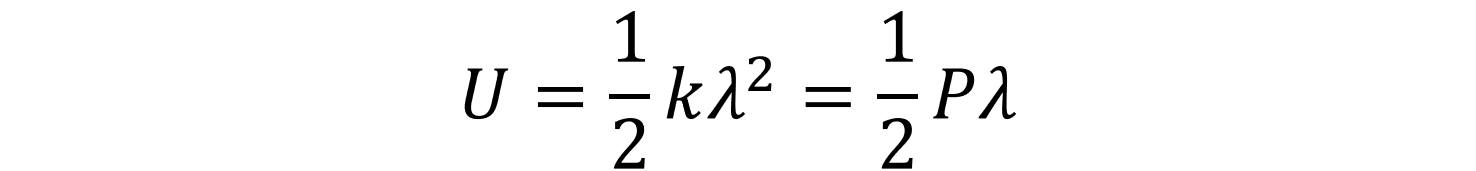
次に、単位体積当たりのひずみエネルギー u を求めます。
式(1.5)の両辺を棒の体積 V で割ると、最終的には式(1.6)の形が得られます。

(1.6)

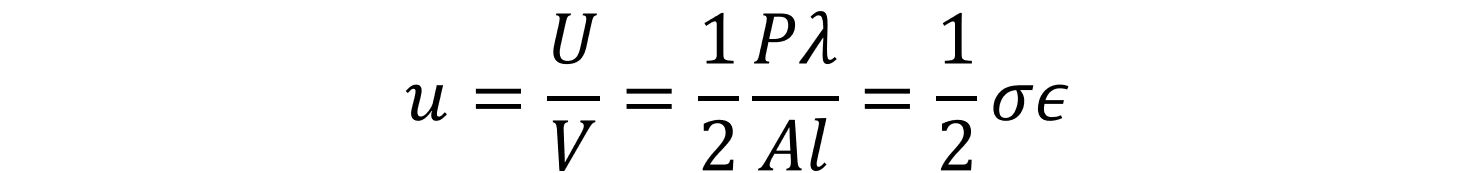
ここで、σ は応力、ε はひずみを表します。有限要素法でのひずみエネルギーの求め方を考えてみましょう。
有限要素法において、荷重や変位は節点に作用しており、内部に蓄えられるひずみエネルギーを考える場合、次式のように、要素に作用する応力やひずみから求めるのが妥当です。

(1.7)

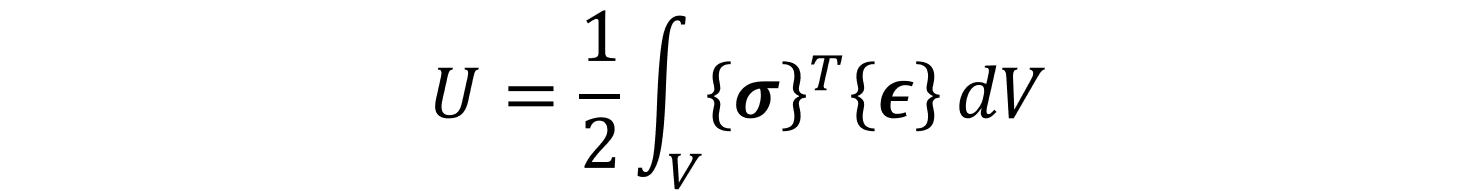
ここで、応力とひずみの関係と、ひずみと変位の関係を整理しておきます。

(1.8)

(1.9)

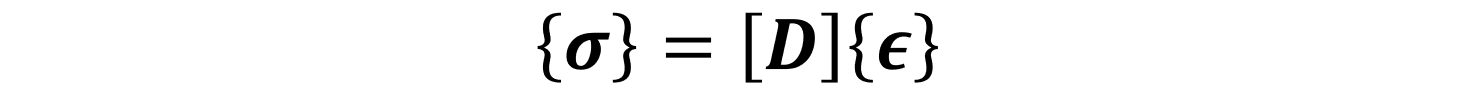
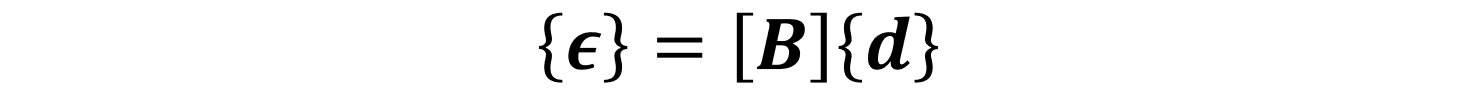
式(1.8)と式(1.9)を式(1.7)に代入すれば、ひずみエネルギーは次式(1.10)のように書き直せます。

(1.10)

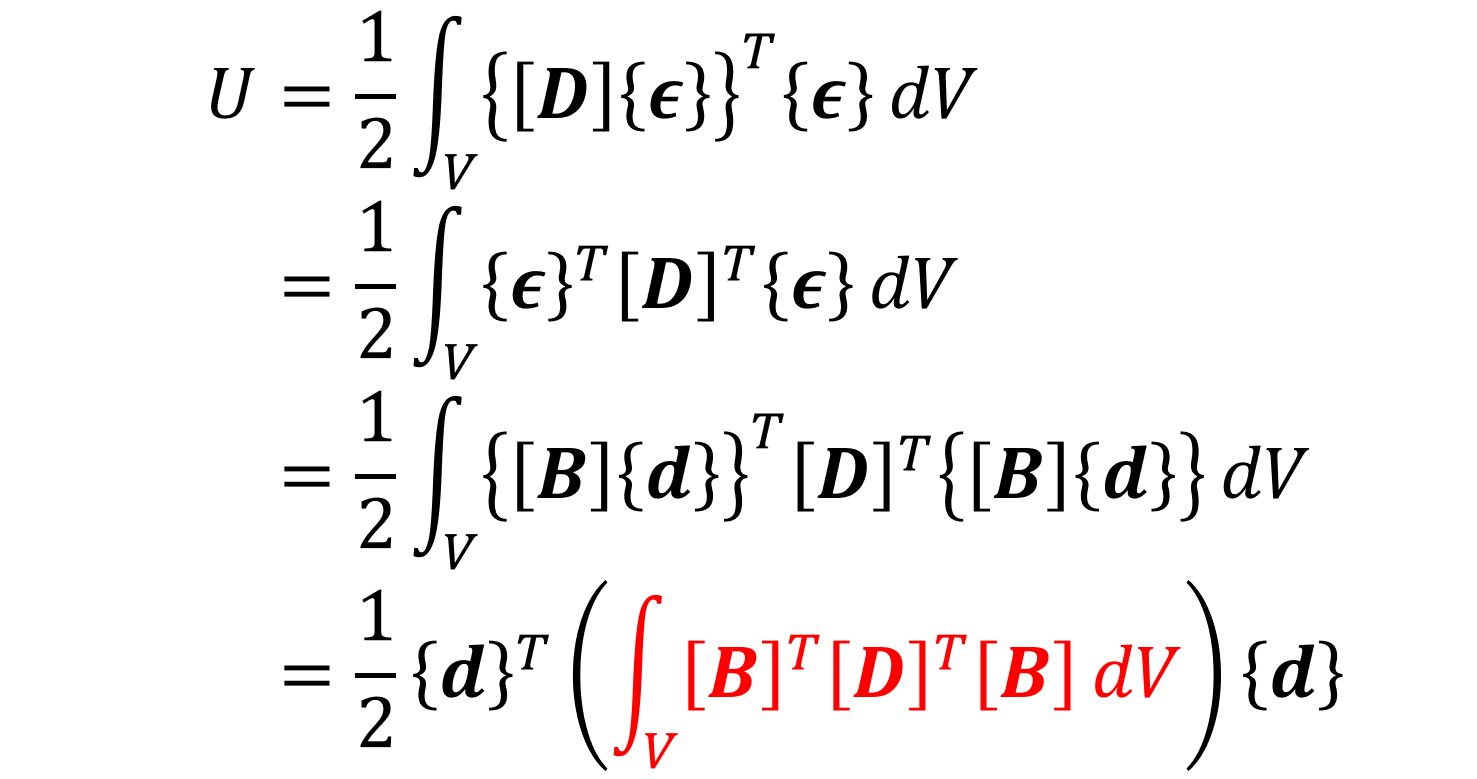
話が長くなるので詳細は割愛しますが、式(1.10)の赤字の部分が、式(1.3)の剛性マトリックスとなっています。
ここを K で置き換えると、式(1.10)は次式のようになります。

(1.11)

式(1.11)が式(1.5)と等しくなっていることがお分かりいただけると思います。
有限要素法ではこのようにしてひずみエネルギーを求めます。

いよいよ(やっと)『剛性最大化』について

前置きが長くなりましたが、ここでようやく『剛性最大化』に触れていきます。『剛性』とは変形のしにくさを表す指標でした。
『ひずみエネルギー』とは変形が生じた際に物体に蓄えられるエネルギーでした。同じ荷重が与えられたとしても、
　『剛性』が大きければ変形が小さいため、『ひずみエネルギー』も小さくなりますし、
　『剛性』が小さければ変形が大きいため、『ひずみエネルギー』も大きくなります。
つまり『剛性』と『ひずみエネルギー』は反比例の関係にあります。従って、『剛性最大化』では、剛性マトリックスをそのまま使うのではなく、『ひずみエネルギー最小化』の問題に置き換えて計算をしています。