【構造】製品設計/強度設計の基本講座シリーズ　vol.3　応力テンソルの不変量と材料強度

2020年06月03日

前回、構造内部に作用している力ベクトルから、応力テンソル（マトリックス）を定義しました。
力ベクトルは３方向の値ですが、評価面に作用する表面力としては、各3方向の面に作用する3方向の力として、3×3 のマトリックスの形で表現されるものでした。
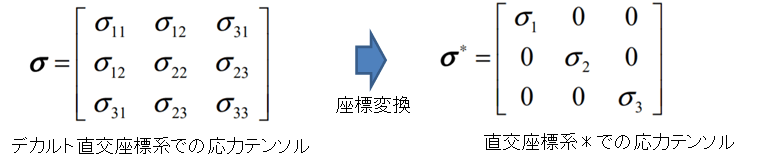
そして、マトリックスを座標変換（座標変換しても物理的意味は変わらない）すると、マトリックスの各応力成分の値が変わり、ある座標方向では、対角項のみ（非対角項が０）の成分で表現できます。
これは、主軸方向の力成分を表しており、3方向の力の本質を表しています。

応力テンソルの不変量

上記で、座標変換により応力成分の値は変わると言いましたが、座標変換しても変わらない量があります。
結果から示しますと、 $Ｉ_{1}$ 、 $Ｉ_{2}$ 、 $Ｉ_{3}$ の3つの量となります。応力成分（ijk の総和規約）であらわしていますが、主応力で表示すると一番右側の項となります。
この量を応力の基本不変量といいます。

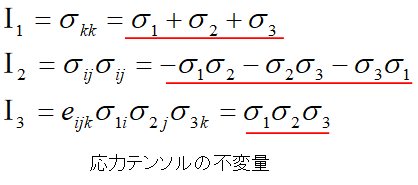
平均応力と偏差応力との分離

ここで、不変量 $Ｉ_{1}$ の 1/3 の値を持った対角行列（平均応力テンソル σm）を定義します。
応力テンソルから平均応力テンソルを引いた残りのテンソルは、偏差応力テンソル（ｓ）と呼ばれます。

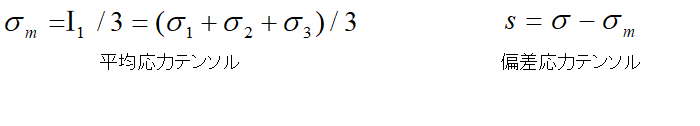
偏差応力テンソルは、固有値が σm だけ小さいだけで、主軸方向は変わりませんので、主応力表現では、以下となります。
この偏差応力テンソルの不変量を改めて $Ｊ_{1}$ ， $Ｊ_{2}$ ， $Ｊ_{3}$ と定義します。

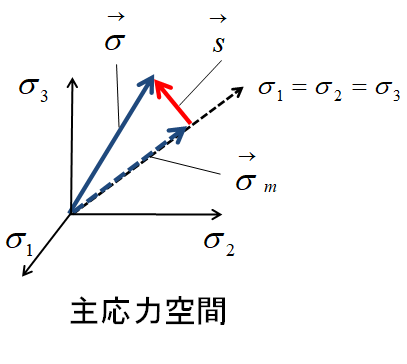
それぞれの関係を、主応力空間（３直交軸が3つの主応力）で、表すと右図になります。
平均応力は、（1,1,1）の方向に一致します。偏差応力は、応力から平均応力を引いたもので、平均応力と直交することから、等方的な応力とは無関係な純せん断応力を表しているといえます。

不変量と材料強度

偏差応力テンソルの３つの量のうち、 $Ｊ_{2}$ はせん断成分の大きさを表しており、この値が材料のある限界を超えるとせん断破損（転移）が起きるとして評価して良さそうです。
更に、一軸引張試験より得られる材料の応力値と直接比較できるように、 vonMisesの式の補正をして定義されたのが、ミーゼスの相当応力です。
定義式から、＋の絶対値を持ち、材料の降伏が生じる応力値として設計で使われています。

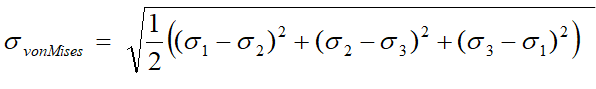
せん断成分の最大値（ $Ｐ_{1}$ － $Ｐ_{3}$ )/2　もせん断損傷に影響しますが、材料の許容せん断応力値はなかなか測定できないので、一軸引張応力値と比較するために、応力強さ（ $Ｐ_{1}$ - $Ｐ_{3}$ ) が用いられます。
更に、主応力値の不変量 $Ｉ_{1}$ は、材料の引張破損、圧縮破損に関係しますので、せん断（転移）損傷よりもへき壊や圧壊が起こりやすい脆性材料に使用されます。

[From N. Sahashi]

全体カテゴリ

製品カテゴリ

Topics
トピックス

SBDプロダクツサービス部
SBDエンジニアリング部

技術コラム