【構造】製品設計/強度設計の基本講座シリーズ　vol.2　マクロな材料の実態強度

2020年05月21日

前回、ミクロの欠陥が起点となり、転位現象によってものが壊れることを紹介しました。
しかし、実際には、ミクロの欠陥をモデル化しその転位現象を解析して強度設計をするわけにはいきません。
欠陥がある程度含まれたマクロな領域での強度が評価出来ればいいわけです。
破壊は面に起きるので、ある面に作用する内力（部材内の断面力のようなもの）の大きさを見積もればいいように思います。
しかし、材料力学の梁部材の断面力（軸力やモーメント）の定義と違って、3次元の任意形状、任意分布を持った断面力を評価するためには、もう少しミクロなレベルの定義が必要になります。

コーシーの応力原理

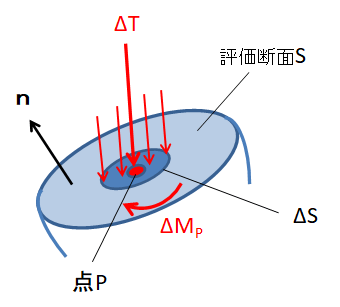
ここで、コーシーの応力原理を紹介します。
ある評価断面内（断面の法線ベクトルを n とします）の面 ΔS に作用している断面力 ΔT を考えます。
その後、ΔS を小さくしていき、点P に集約していくと、その状況で、ある点に作用する内力ベクトル T(n) が定義できます。
また、点P回りのモーメントMp は 0に収束していきます。

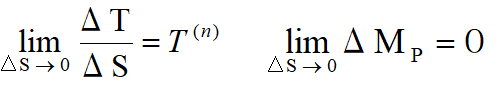
断面と直交面との力の釣り合い

次に、ここで定義された T(n) と、微小領域での力のつり合いを考えます。簡単のため、2次元で考えてみます。

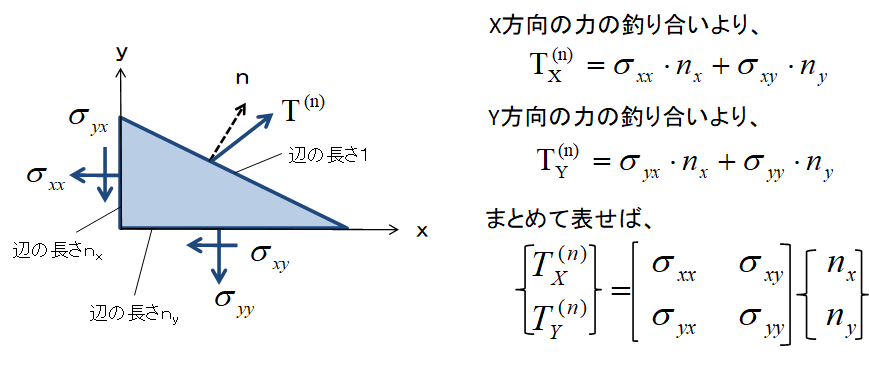
このように、ある点での内力ベクトル T(n) は、評価断面の法線ベクトル n とそれ以外の項に分離されます。
この分離された項が法線ベクトルに依存しない、内力ベクトルをある直交座標系で表現し直した内力状態を表しているものとなります。
ここでの、内力ベクトルは単位面積（2次元の場合は単位長さ）を表していますので、単位面積当たりの力の大きさの直交座標表現になっています。
これが、「応力」と定義され、マトリックスの形で表されます。

応力マトリックスの特徴

また、内力ベクトル T(n) が、法線ベクトル n の方向と一致する場合、下式となります。
これは、固有値の式と同形式となり、斜面に作用するベクトルが法線成分のみ（せん断成分が０）となる方向が存在することを示しています。
その方向を「主軸方向」、法線方向のベクトルを「主応力」、と呼びます。

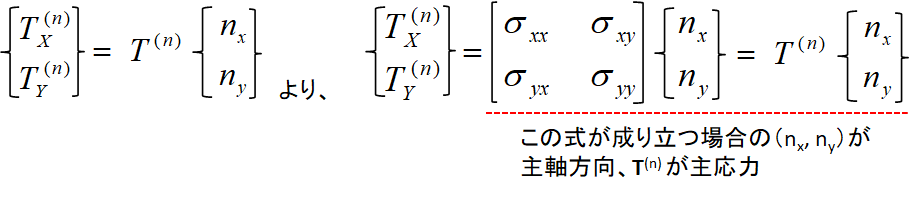
3次元で、同様に力のつり合い式を考えれば、3×3のマトリックスの形として、応力が定義されます。3次元では、3つの主応力、3つの主軸方向（3方向は直交している）が存在します。
力の本質は、直交する3方向（固有方向）から引張られたり、押されたりする状態となっているといえます。

数学的には、力の方向と面の方向の成分を持った2階のテンソル形式となります。また、モーメントの釣り合い条件から、対称行列となり、上式の様に主軸に一致した直交座標系では、対角行列となります。

これらの意味や強度評価へのつながりは、また次回に続きます。

[From N. Sahashi]

全体カテゴリ

製品カテゴリ

Topics
トピックス

SBDプロダクツサービス部
SBDエンジニアリング部

技術コラム