お気軽にお問い
前回、速度勾配テンソル
を定義し、
として対称部分 と反対称部分 に分解しました。
は変形速度テンソルと呼ばれ、微小ひずみの定義と同様の形式で各軸方向、及び、せん断方向の変形の速度を表しました。
また、 はスピンテンソルと呼ばれ、回転の速度を表します。
ここでは、 についてもう少し考えます。
COLUMN
技術コラム
【構造】製品設計/強度設計の基本講座シリーズ vol.11 スピンテンソルのイメージ
スピンテンソルのイメージ
まず、ある領域全体が1点 を通る単位ベクトル を軸として右ねじ回りに角速度
で回転している状態は、以下の点 に関する回転軸ベクトル で表されます。
下図参照。
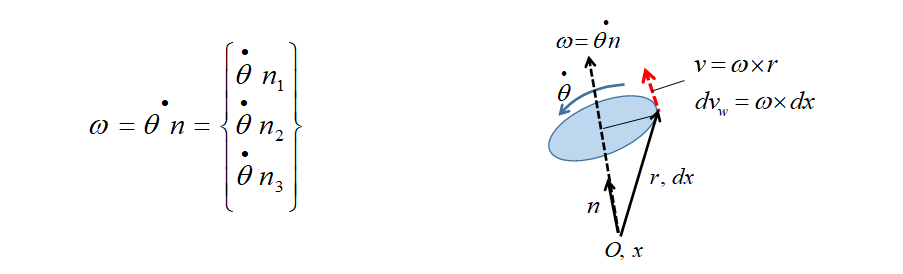
この時、点 から見て、位置 にある点の速度ベクトルは、
の様に外積によって表されます。
これに対応して考えると、スピンテンソルの寄与分の速度
も以下の様に外積で表してみます。
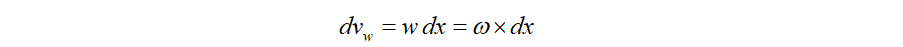
この時、 の具体的成分は以下となり、これはスピンテンソルの各成分と同じになっています。
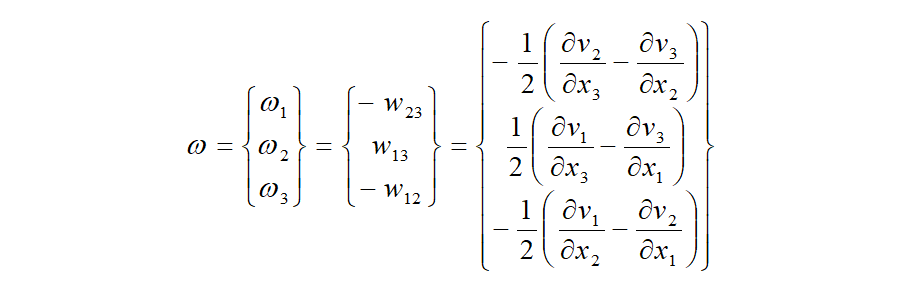
これは、回転軸ベクトル は、スピンテンソルの成分で表されることが分かり、スピンテンソルも回転軸ベクトルと同様の作用があることが分かります。
つまり、 は と同じ作用をし、微分ベクトル を回転運動成分に由来する速度増分ベクトルに変換するテンソルであることが分かります。
スピンテンソルと呼ばれる理由です。
有限ひずみの物質時間微分
変形速度の次に、ひずみの速度も考える必要があります。
以前定義した有限ひずみのラグランジュグリーンひずみ 及び、オイラーアルマンジひずみの物質微分を考えてみます。
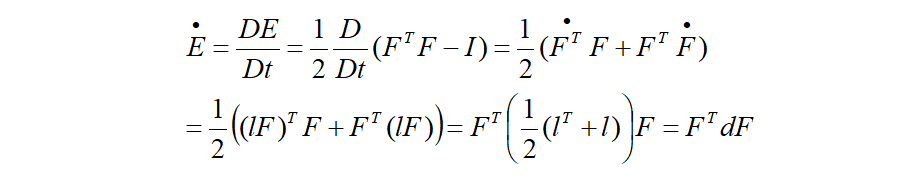
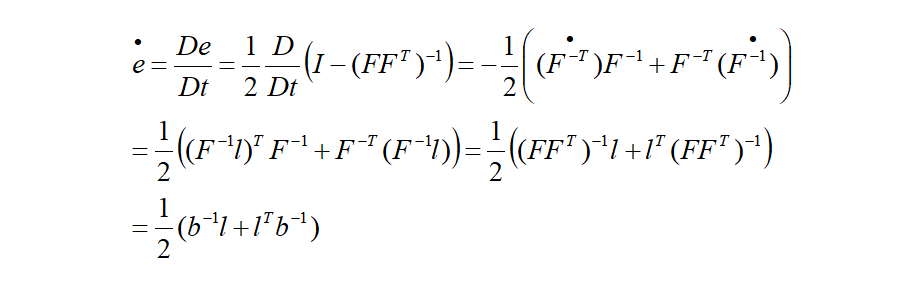
ここで、以下の関係を使っています。
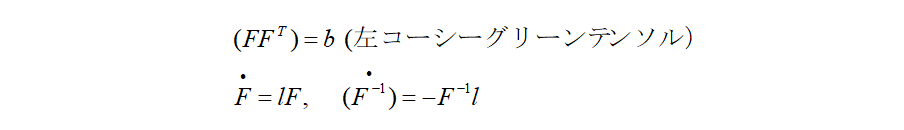
ヤコビアンの物質時間微分
変形、ひずみの速度の他、連続体内部における局所的な体積、面積の時間変化も考慮しなければなりません。
そのために、ヤコビアン
の 物質時間微分を考えます。
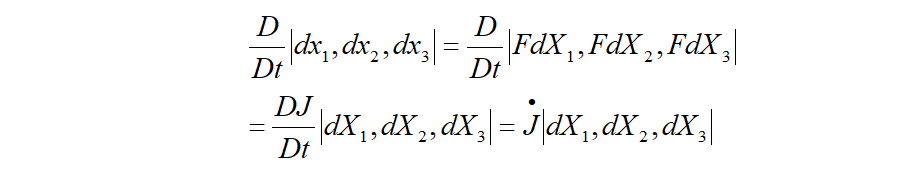
更に、上式の最終項を変形していくと、
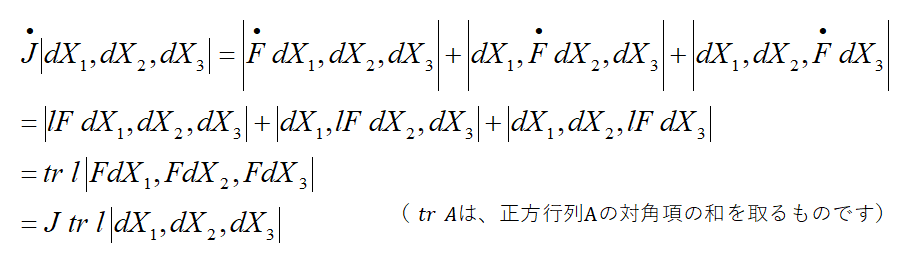
結果、上式より、
は任意なので、ヤコビアンの物質時間微分は、以下のの関係を得ます。
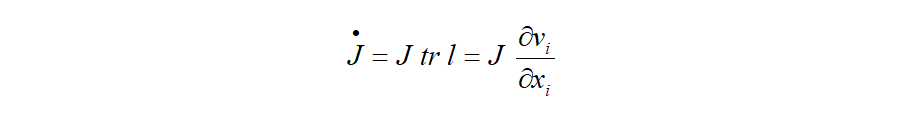
今回まで見てきた各物理量の物質時間微分は、動的な解析だけでなく非線形の増分解析の時に必要となってきます。
[From N. Sahashi]
第1・第3木曜日配信！
SBDメールマガジンより、
最新の技術コラムをお届けします。
Analysis Case
解析事例
Analysis Case
解析事例
解析事例
Topics
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2024年10月08日
2024年08月27日
2024年08月26日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2024年10月01日
2024年10月01日
2024年09月24日
Topics
トピックス
トピックス
イベント・セミナー
シミュレーションに関するイベント・セミナー情報をお届けいたします。
2024年10月08日
2024年08月27日
2024年08月26日
トレーニング
SBD製品各種の操作トレーニングを開催しております。
2022年11月02日
2022年03月04日
2022年03月04日
技術コラム
シミュレーションに関する基礎知識や、製品の技術的なノウハウが満載の技術コラムをお届けいたします。
2024年10月01日
2024年10月01日
2024年09月24日
