【構造】ひろこの部屋vol.12　解析事例　瓶の蓋のポコポコ

2022年07月07日

今回解析するのは瓶の蓋で開封すると凹凸が逆転するものです。未開封の状態が確認できるためセーフティボタンと呼ぶそうですが、あの中心部を触るのが好きで、開封後にポコポコ鳴らして楽しんでいます。瓶ごとにクリック感が違うのも奥深く私は桃屋の蓋がお気に入りです。

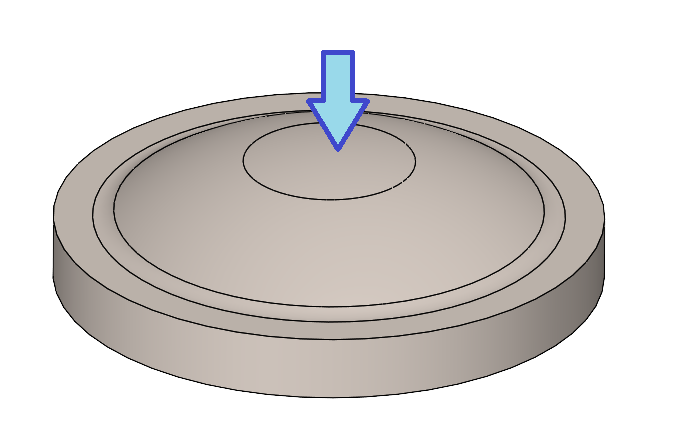
さて、無駄話はほどほどにセーフティボタンを解析する際の解析種別を考えましょう。力はゆっくりと加える静解析、凹凸の逆転を確認する場合は変形形状が視認できる程度に大きいので幾何学非線形解析が適していそうです。

荷重と変位グラフの観察

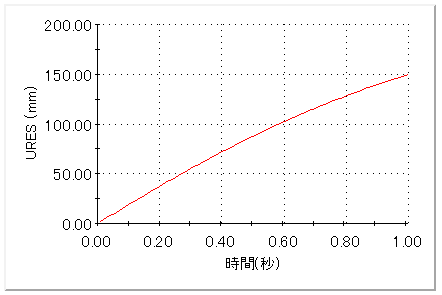
幾何学非線形といえば、前回紹介した薄板の曲げ問（https://www.sbd.jp/column/kozo_hiroko_vol11_sheet-bending-problem.html）があります。薄板の曲げ問題の非線形解析ではステップごとに荷重を増やす計算を行っていました。右図は時間ステップに対する変位のグラフです。時間に応じて荷重が線形に増やされるため、荷重値の増加に対して変位が右肩上がりに増えているのが分かります

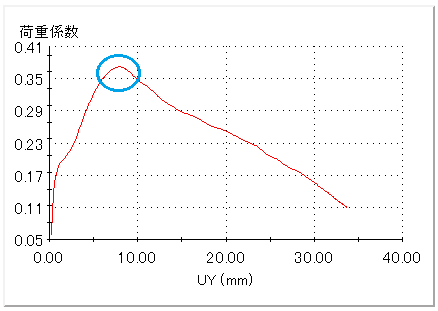
それに対し、セーフティボタンのモデルでは荷重と力の関係が単純増加や単純減少にはなりません。右図は変位に対する荷重係数のグラフです。上のグラフとXY軸の意味合いが入れ替わっているのでご注意ください。青丸部分を境に荷重が減少に転じているのが確認できます。この部分で構造が不安定になり座屈が発生します。

非線形の進捗をコントロールする増分制御法

非線形解析では計算を進めるための制御方法が複数用意されています。それぞれの制御方法に従い解析ステップが進められ、定められた条件が満たされると計算が終了します。
ここでは3つの制御法を紹介します。

　●荷重増分法：外部荷重や強制変位を時間刻みで増加させ構造物の変化を確認する
　●変位増分法：指定したポイントの変位が指定した値になるまで荷重を増加させる
　●弧長増分法：荷重と変位のグラフの弧の長さに応じて制御し変位量やステップ数が基準値に到達するまで計算を行う

画像出典：SOLIDWORKS Simulaitonオンラインヘルプ

荷重増分法や変位増分法は荷重と変位の値が単純増加あるいは単純減少の計算しか扱うことができません。それに対し弧長増分法では荷重と変位の増減が変化する問題でも適応できるため、座屈現象の解析によく使用されます。

画像出典：SOLIDWORKS Simulaitonオンラインヘルプ

解析結果

弧長増分法を使って計算した瓶の蓋（セーフティボタン）の解析結果です。
解析は軸対称2次元モデルで計算、結果のみ３D表記をしています。

下図の真ん中の図がモデルの不安定になる点で弧長増分法以外の手法では直前で計算が停止します。

■応力結果

■変位結果

最後に

次回は、非線形解析の3種類目、境界非線形をご紹介します。

[From H. Horiuchi]

全体カテゴリ

製品カテゴリ

Topics
トピックス

SBDプロダクツサービス部
SBDエンジニアリング部

技術コラム