COLUMN

技術コラム

【構造最適化】固有振動数の最適化事例　vol1　重み付け無しでの形状最適化

2021年05月06日

今回は単振動の振動数式を元に固有振動数の最大化について、事例を交えて紹介していきます。

固有振動数について

ばね定数kのばねに質量mのおもりをつけて釣り合った状態にしたのち、ある長さA だけ引っ張ってから手を離すと、おもりは振幅をAとする単振動を行います。
この単振動の振動数fは次式で求められます。

（１）

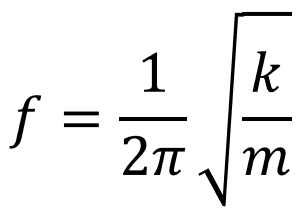
ある物体の固有振動数を、直接、式(1)で評価することはできませんが、一般に、剛性(k)が大きく、質量(m)が小さくなるほど、固有振動数は大きくなることがわかります。
今回はこの式に基づいた固有振動数の最大化について、事例を交えて紹介していきます。

計算事例

Fig.1に計算事例に用いた機械部品を示します。まずはSOLIDWORKS Simulationの固有値解析にて、この機械部品の固有振動数を求めます。固定箇所は鍵型の穴の内側の面です。

Fig.1 計算に用いた機械部品の鳥瞰図

固有値解析の結果をTable.1に示します。
仮に、今回、目標とする固有振動数が700 Hz以上として、最適な形状を求める手順を紹介していきます。

Table.1 固有値解析の結果一覧(モード形状10まで)

固有振動数の最適化～Step. 1 重み付け無しでの形状最適化～

Table.1に示した結果から、目標とする700 Hz以下のモード形状を探します。
今回のケースであれば、モード形状1が該当します。
また、モード形状2と3は700 Hzより大きいですが、最適な形状を探索する過程でこれを下回るようなことがあるといけません。
従って、今回は、Fig.2に示すモード形状1、2および3の変形パターンを見ながら、最適形状を計算します。


(a)	(b)	(c)

Fig.2 固有値解析のモード形状 (a)モード形状1 (b)モード形状2 (c)モード形状3

まずは静解析において、Fig.2の変形モードを再現できる荷重パターンを見つけます。
Fig.3にそれぞれの荷重パターンを示します。
ここでは変形を再現できれば良いため、荷重値、トルク値はデフォルトの1 Nおよび1 Nmを用いました。


(a) モード形状1
力：1 N

(b) モード形状2
力：1 Nm

(c) モード形状1
力：1 N

Fig.3 モード形状を再現する荷重パターン

最適化の条件をTable.2に示します。
まずはいずれの荷重パターンに対しても元の剛性の100%を維持する、すなわち荷重パターンに対する重み付け無しで最適な形状を求めます。
これは傾向を見るための解析なので、メッシュは粗く、数分で計算が終了するようにしました。
そのときの結果をFig.4に示します。

Table.2 最適化における目的関数と制約関数の一覧


(a) 最適化前	(b) 最適化後

Fig.4 最適化前後の結果

Fig.4は粗いメッシュで計算した結果ですので、形状の滑らかさ等は目を瞑ってこのまま議論を進めます。
Table.2に示した目的・制約関数で計算すると、Fig.4(b)のような結果が得られました。
この形状に対し固有値解析を行い、得られた固有振動数の一覧をTable.3に示します。

Table.3 最適化後の固有値解析の結果一覧(モード形状10まで)

Table.3に示した通り、モード形状1、2および3のいずれにおいても元の形状よりも固有振動数が大きくなっているのがわかります。
これはすべての制約条件である元の剛性100%を維持しながら、質量が元の約90%と軽くなっており、式(1)と同じ傾向を示しています。
最適化後の固有振動のモード形状はFig.5に示す通り、もとのモード形状と同じであることが確認できています。


最適化前
(a) モード形状1	(b) モード形状2	(c) モード形状3


最適化後
(d) モード形状1	(e) モード形状2	(f) モード形状3

Fig.5 最適化前後での変形モードの比較

以上の結果から、『剛性を維持しながら軽量化』と『固有振動数の増加』はほぼ等価であることが示されました。

次回予告

次回は固有振動数を700 Hz以上にするためのStep 2として、重み付けありでの形状最適化についてご紹介します。

[From K.Takabatake]

モード形状	固有振動数 Hz
1	485.67
2	1,055.8
3	1,211.7
4	3,458.4
5	5,608
6	6,281
7	7,396
8	7,645.4
9	8,458
10	10,423

目的	以下の制約条件を満たす中で質量が最小になる形状を求める
制約１	Fig.3(a)の荷重パターンに対して剛性を100%維持する
制約２	Fig.3(b)の荷重パターンに対して剛性を100%維持する
制約３	Fig.3(c)の荷重パターンに対して剛性を100%維持する

モード形状	固有振動数 Hz　｜　元の固有振動数 Hz
1	533.42　｜　485.67
2	1159.8　｜　1,055.8
3	1438.2　｜　1,211.7
4	3491.6　｜　3,458.4
5	4539.2　｜　5,608
6	6554 　｜　6,281
7	6782.1　｜　7,396
8	7124.4　｜　7,645.4
9	7701 　｜　8,458
10	8431.9　｜　10,423