今回は、過去のメルマガで好評だった記事から「ディップの流体力学 - チョコレートフォンデュの解析」についてご紹介致します。
＊＊＊＊＊

ディップに関する流体力学をご紹介します。
固体を液体にディップする過程はディップコーティングと呼ばれ、応用範囲が広いです。
今回はその例として、マシュマロをチョコレートフォンデュする過程をシミュレーションしてみました。
マシュマロを上げるスピードによって、チョコレートの付着量が変わります！
理論的には、ゆっくり引き上げるよりほぼ一瞬で引き上げた方がチョコレートがよくくっつきます！！

目的

チョコレートフォンデュを流体解析ソフトウェアParticleworksを用いて検証します。
マシュマロをあげる速度の依存性を検証します。

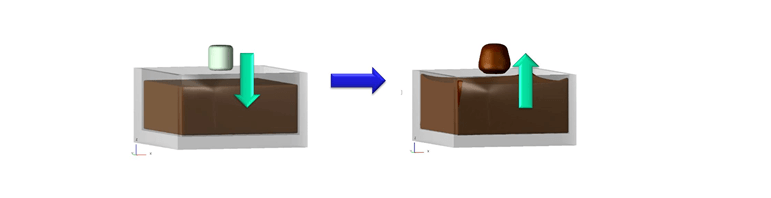
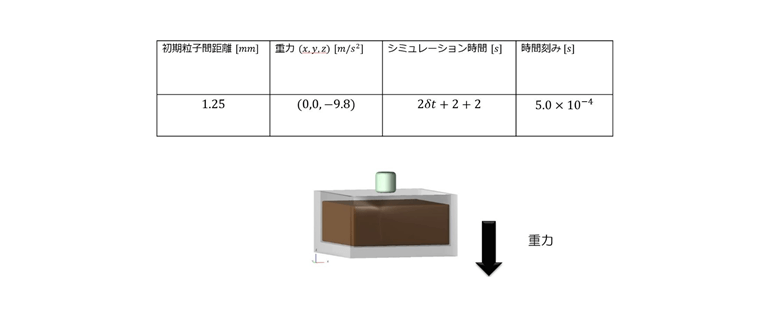
解析形状

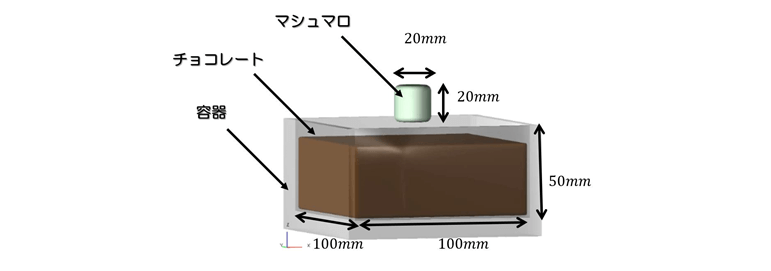
解析モデル

■　流体特性 ［1］
チョコレートは、粘性がせん断速度に依存する非ニュートン流体です。

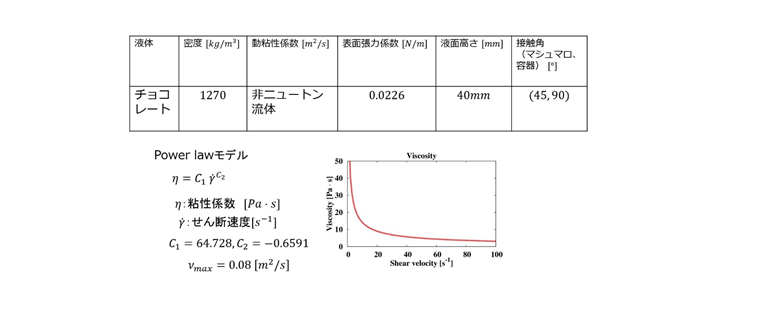
※マシュマロとの接触角は不明なため、今回は45度で設定しています。
　ただし、毛管数が大きいので、接触角による結果の依存性は小さいと考えています。（参照：考察）
　容器との接触角は、マシュマロへの付着量に影響しないので、90度に設定しています。
※νmax：低せん断領域での動粘性係数のカットオフ（最大値）です。

Power law モデルでは、せん断速度が0のとき動粘性係数が無限大になり発散してしまうため、低せん断領域ではカットオフ値（最大値）を設定します。

■　移動定義
等速で液体にディップしたあと、2s間液体中で静止し、その後等速で引き上げています。
引き上げ速度（=ディップ速度）を5パターン解析しています。

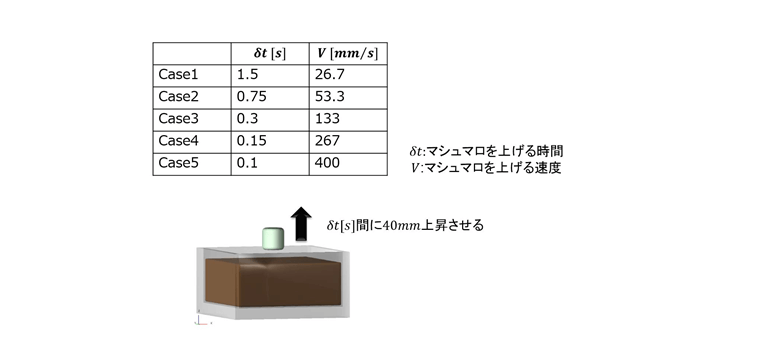
■　そのほか

結果

Case1（引き上げ速度v_1=26.7[m/s]）を基準に比較しています。

■　粒子表示

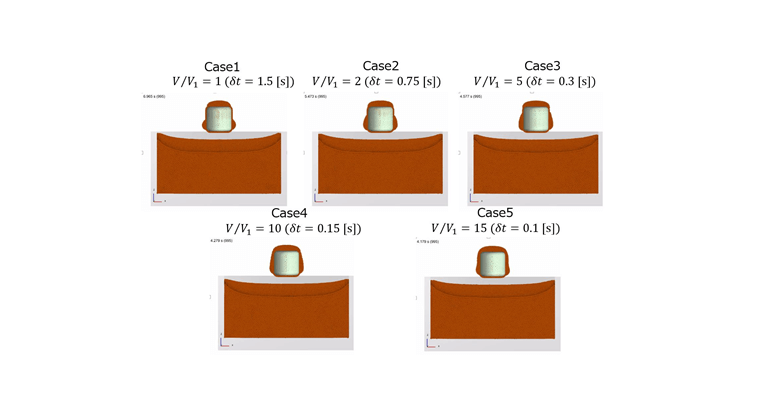
■　動粘性係数表示

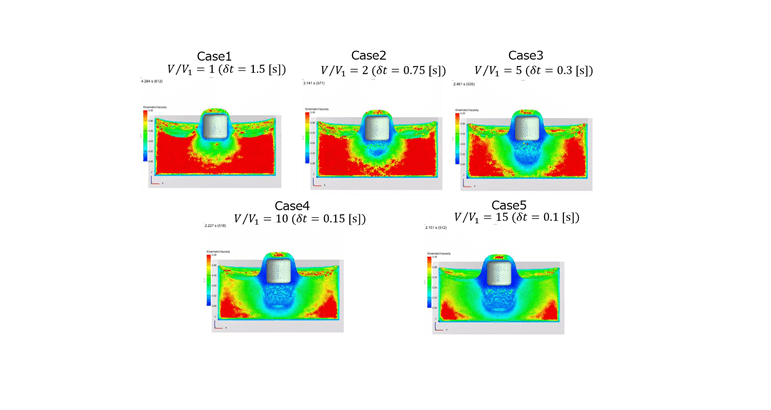
■　レンダリング表示

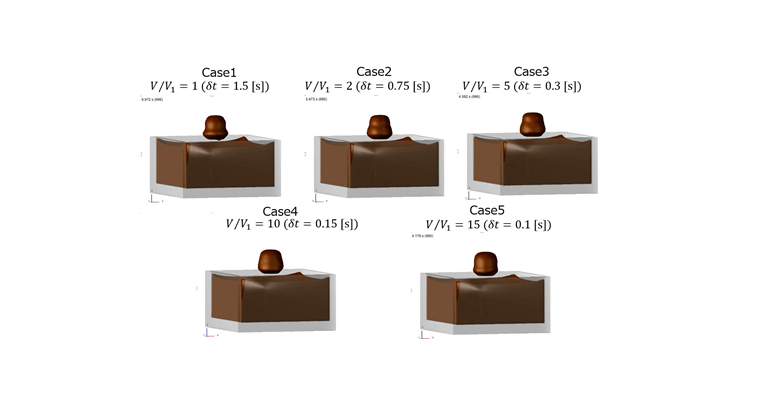
考察

■　付着量
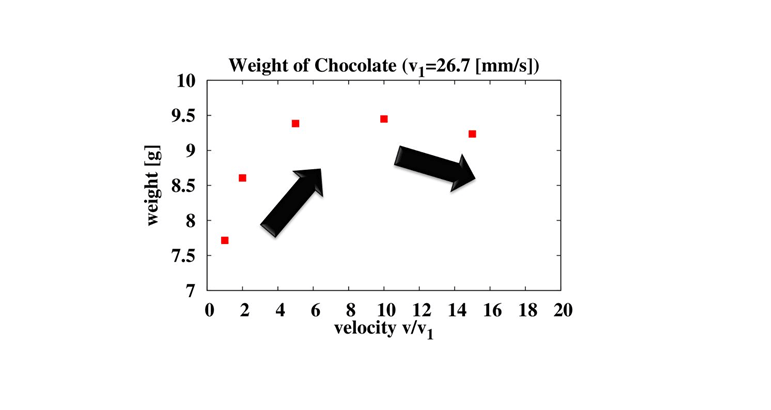
マシュマロへのチョコレートの付着量を算出します。

速度が小さい時
　速度が速くなるほど付着量が増大します。
速度が大きい時
　ある速度で付着量が極大になり、その後付着量が減少します。

■　定性的議論
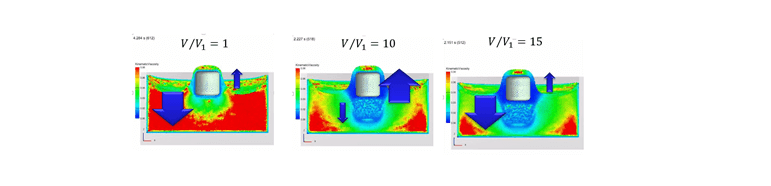
低速度：V<<1
　速度が小さいときは、低速かつ高粘性のため、下の流体にひっぱられやすくなります。
　逆に速度が速くなると、速度の効果によって上に液体がひっぱられやすくなります。
　また粘性が低くなり、上の固体にもひきずられやすくなります。
　固体周辺の広い領域の液体が上にひきずられやすくなるためです。

高速度：V>>1
　速度が速すぎると、上の固体にくっつきません。
　固体周辺のみの液体のみが上にひきずられやすくなるためです。

■　定量的議論（無次元数）
無次元数 [2]
　Reynolds数(Re)、毛管数(Ca)、毛管長( ${\kappa }^{-1}$ )を使用します。
　Reynolds数は粘性と慣性、毛管数は粘性と表面張力、毛管長は表面張力と重力のどちらが力として支配的かを表すことができます。
　定義は、以下です。

Landau-Levich-Derjaguin's law [2,3]
　ディップに関する理論で有名な法則としてLandau-Levich-Derjaguin's lawがあります。
　固体を液体にディップしたときの付着液の厚みeを無次元数だけで求めることができます。
　レイノルズ数が小さいこと、潤滑近似（薄膜の流れでよく行われる近似）が成立していることを仮定しています。
　また算出方法は、粘性力と重力がつりあうと仮定して、算出できます。
　毛管数が大きいときは以下です。（Derjaguin's law)

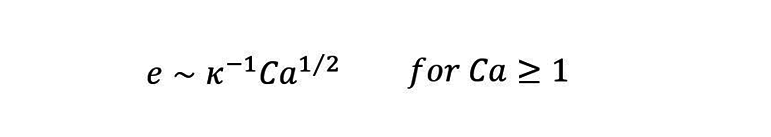
この法則を用いて、付着量V_dipのオーダーを見積もると以下です。

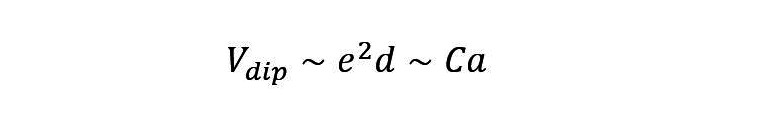
今回は粘性が大きいため、毛管数が大きい状況です。
ちなみに、参考までに毛管数が小さいときは以下です。(Landau-Levich-Derjaguin's law)

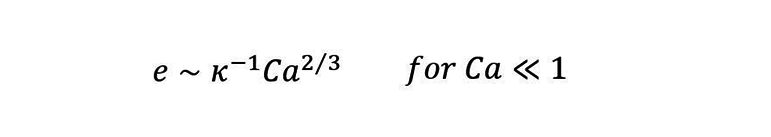
これは表面張力の影響が大きいときに関係してきます。
粘性力と表面張力がつりあうと仮定すると導出できます。

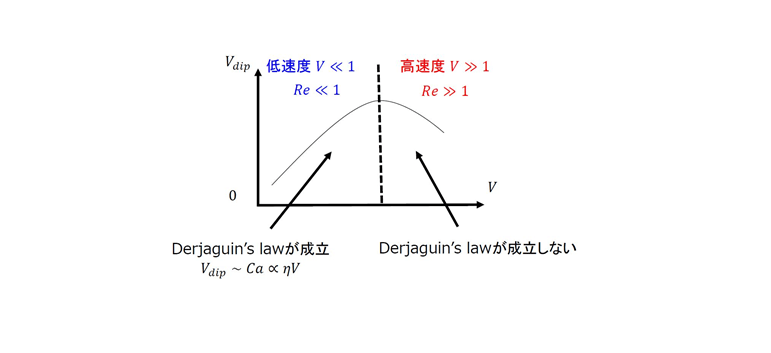
まとめ

流体力学を用いたチョコレートフォンデュの解析を行い、マシュマロの引き上げ速度依存性によるチョコ付着量を調べました。

低速度
　速度が小さいところでは、速度が速くなると付着量が増大します。
　付着量は毛管数に比例（Derjaguin’s lawが成立）

高速度
　速度が大きくなると、極大を境に付着量が減少します。
　付着量は、高速度ではDerjaguin’s lawが成り立たない

参考文献

[1] Adam K. Townsend “The fluid dynamics of chocolate fountains”
Pierre-Gilles de Gennes, Francoise Brochard-Wyart, David Quere
[2] ドゥジェンヌ、ブロシャール-ヴィアール、ケレ著、奥村剛訳 “表面張力の物理学”, 吉岡書店
[3] L. Landau and B. Levich, Acta Physicochim. USSR 17, 42 (1942), B. V. Derjaguin, , Acta Physicochim. USSR 20, 349 (1943), B. V. Derjaguin and S. M. Levi, Film coating theory (The Focal Press, London, 1964)

[原文： ひっつきもっつき 　転載：R.Taniguchi]