【粉体】Vol.4　粒子径分布(粒度分布)

2020年04月16日

粉体は粒子径が粒子毎に異なるため、多くの場合は各粒子の粒子径をまとめて分布として管理します。この分布のことを「粒子径分布(粒度分布)」と呼びます。粒子径分布は、取得したデータによって「頻度分布（ヒストグラム）」、「積算分布」で表記されます。

頻度分布（ヒストグラム）

頻度分布（ヒストグラム）とは、階級(粒度)毎の粒子の割合を表示したものです。例として篩による粒子径の測定について説明します。試料200gを目開きが異なる10枚の篩網を用いて、篩網の上に残った粉体量を集計した結果を表にまとめました。1000μmの目開きの篩網を通過できなかった粉体が2g存在しており、この粉体は1000μmより大きい粒子径を持つことになります。全体は200gなので、1000μmより大きい粒子径を持つ粒子は1%となります。次に1000μmの目開きの篩網を通過して、900μmの目開きの篩網の上に残った粉体は6gとなります。この粉体の粒子径は、900μmより大きて1000μm以下であることが分かり、この範囲の粒子径を持つ粒子は全体の3%となります。この様にすべての篩の上に残った粒子の割合をグラフで示したものが頻度分布（ヒストグラム）となります。

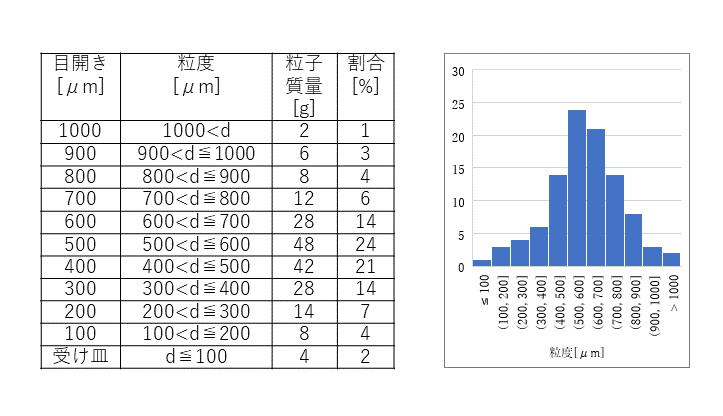
頻度分布（ヒストグラム）で注意しなければならないのは、「1000μmより大きい」や「900μmより大きく1000μm以下」というように各データに幅があるということです。つまり、特定の粒子径の割合を示しているのではありません。
　頻度分布（ヒストグラム）では、最も多い粒子径の範囲や粒子径の広がり（ばらつき）が一目でわかります。一方で、これらの値は区間の設定に依存するため、読み取る際に注意が必要となります。例えば、先ほどのデータの区間を100から250に変更した結果が下図になります。この結果では475μm（区間(350,600]の中央値)にピークがあるように見えますが、実際には、区間(500,600]にピークがあります。このように区間の設定によって読み取れる情報が異なります。

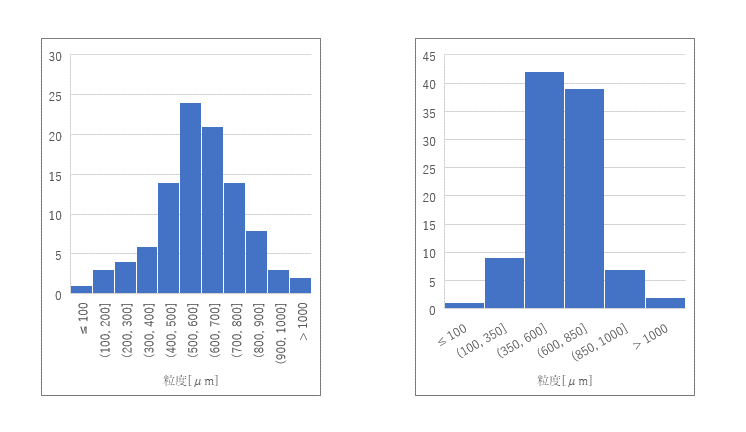
積算分布

積算分布とは、ある閾値以下（以上）の粒子径をもつ粒子の割合を表した分布のことです。閾値以下を集計した場合、「ふるい下積算分布」と言い、閾値以上を集計した場合、「ふるい上積算分布」と言います。ここからは、ふるい下積算分布に絞って説明していきます。閾値が無限に小さい場合、その閾値以下の粒子径をもつ粒子は存在しないため、0%となります。一方で、閾値が無限に大きい場合、すべての粒子が含まれるため100%となります。頻度分布（ヒストグラム）で使用した例を用いると以下のような分布となります。

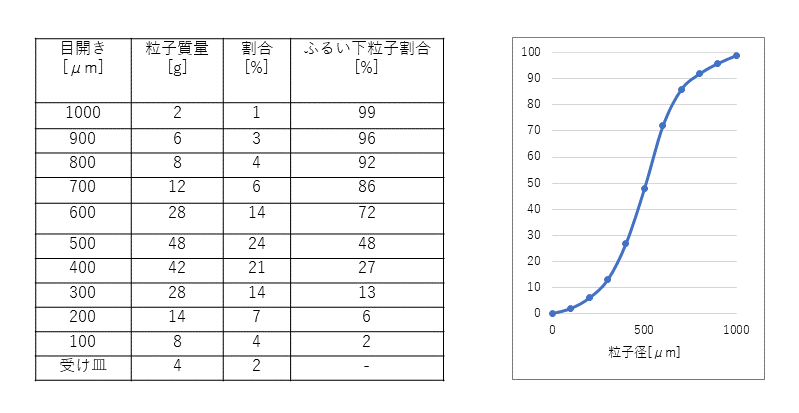
積算分布の特徴は、頻度分布（ヒストグラム）と異なり、区間の設定に依存しない分布になることです。そのため、誰が集計しても同様の分布を取得することができます。一方で、ヒストグラムのように最も多い粒子径の範囲を直接読み取ることが難しくなります。積算分布では、粒子径の割合は、グラフの傾きで表現されます。上の例では、傾きが最も大きい500μm付近が最も多く含まれていることが分かります。積算分布の値が50%になる粒子径のことをD50（メジアン径）と呼びます。その他にも積算分布の値に従って、10％, 90%の粒子径をD10, D90と表記されます。

[From K. Yamaguchi]

全体カテゴリ

製品カテゴリ

Topics
トピックス

SBDプロダクツサービス部
SBDエンジニアリング部

技術コラム